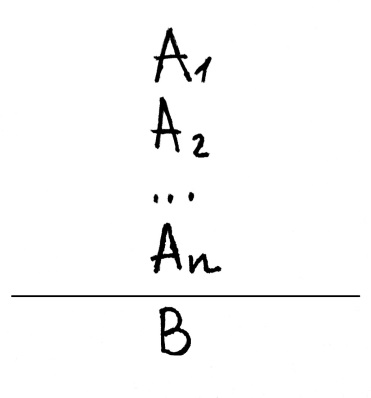данное умозаключение по форме является
Умозаключения. Виды умозаключений
Свойства основных понятий раскрываются в аксиомах – предложениях, принимаемых без доказательства.
Например, в школьной геометрии есть аксиомы: «через любые две точки можно провести прямую и только одну» или «прямая разбивает плоскость на две полуплоскости».
Система аксиом любой математической теории, раскрывая свойства основных понятий, дает их определения. Такие определения называют аксиоматическими.
Доказываемые свойства понятий называют теоремами, следствиями, признаками, формулами, правилами.
Доказать теорему А
Доказательством в математике называют конечную последовательность предложений данной теории, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предложений этой последовательности по правилам логического вывода.
В основе доказательства лежит рассуждение – логическая операция, в результате которой из одного или нескольких взаимосвязанных по смыслу предложений получается предложение, содержащее новое знание.
В качестве примера рассмотрим рассуждение школьника, которому надо установить отношение «меньше» между числами 7 и 8. Учащийся говорит: «7 1
Поэтому выводы, полученные с помощью неполной индукции, необходимо либо доказывать, либо опровергать.
Пример 3. При обучении делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значение выражения 12 : 4, следует узнать, на какое число надо умножить делитель 4, чтобы получить делимое 12. Известно, что 4
Данный пример – это пример рассуждения по аналогии.
Под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.
Данное умозаключение по форме является
1. хНПЪБЛМАЮЕОЙЕ: ПРТЕДЕМЕОЙЕ, УФТХЛФХТБ, ЛМБУУЙЖЙЛБГЙС.
йУФЙООПУФШ Й РТБЧЙМШОПУФШ НЩУМЙ.
уФТХЛФХТБ ХНПЪБЛМАЮЕОЙС
фТБДЙГЙПООЩК ДТЕЧОЕЗТЕЮЕУЛЙК УЙММПЗЙЪН:
2. рлу: ПРТЕДЕМЕОЙЕ, УФТХЛФХТБ, ПВЭЙЕ РТБЧЙМБ.
бЛУЙПНБ УЙММПЗЙЪНБ
пВЭЙЕ РТБЧЙМБ рлу.
I. рТБЧЙМБ ФЕТНЙОПЧ:
1) Ч УЙММПЗЙЪНЕ ДПМЦОП ВЩФШ ФПМШЛП 3 ФЕТНЙОБ
фЕТНЙО н ДПМЦЕО ВЩФШ ПДОЙН Й ФЕН ЦЕ РПОСФЙЕН Ч ПВЕЙИ РПУЩМЛБИ, ЙОБЮЕ РПМХЮЙН ПЫЙВЛХ, ОБЪЩЧБЕНХА «ХЮЕФЧЕТЕОЙЕН ФЕТНЙОПЧ».
2) УТЕДОЙК ФЕТНЙО ДПМЦЕО ВЩФШ ТБУРТЕДЕМЕО ИПФС ВЩ Ч ПДОПК ЙЪ РПУЩМПЛ.
еУМЙ УТЕДОЙК ФЕТНЙО ОЕ ТБУРТЕДЕМЕО ОЙ Ч ПДОПК ЙЪ РПУЩМПЛ, ФП ПФОПЫЕОЙЕ НЕЦДХ ЛТБКОЙНЙ ФЕТНЙОБНЙ Ч ЪБЛМАЮЕОЙЙ ПУФБЕФУС ОЕПРТЕДЕМЕООЩН.
3) ФЕТНЙО, ОЕ ТБУРТЕДЕМЕООЩК Ч РПУЩМЛБИ, ОЕ НПЦЕФ ВЩФШ ТБУРТЕДЕМЕО Ч ЪБЛМАЮЕОЙЙ.
рТЙ ОБТХЫЕОЙЙ ЬФПЗП РТБЧЙМБ ЧПЪОЙЛБЕФ МПЗ. ПЫЙВЛБ «ОЕЪБЛПООПЕ ТБУЫЙТЕОЙЕ ФЕТНЙОБ».
чУЕ РЕДБЗПЗЙ ЧПУРЙФБООЩ
пО ОЕ РЕДБЗПЗ
пО ОЕЧПУРЙФБО
II. рТБЧЙМБ РПУЩМПЛ:
1) йЪ ДЧХИ ПФТЙГБФЕМШОЩИ РПУЩМПЛ ЪБЛМАЮЕОЙЕ УДЕМБФШ ОЕМШЪС (ИПФС ВЩ ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОПК).
оЙ ПДЙО УФХДЕОФ ОЕ СЧМСЕФУС РТЕРПДБЧБФЕМЕН
CФХДЕОФ йЧБОПЧ ОЕ СЧМСЕФУС РТЕРПДБЧБФЕМЕН
?
2) йЪ ДЧХИ ЮБУФОЩИ РПУЩМПЛ ЪБЛМАЮЕОЙЕ ОЕ УМЕДХЕФ (ИПФС ВЩ ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ПВЭЙН УХЦДЕОЙЕН).
йЪ ДЧХИ ЮБУФОЩИ РПУЩМПЛ РТБЧЙМШОПЕ ЪБЛМАЮЕОЙЕ УДЕМБФШ ОЕЧПЪНПЦОП.
рТЙНЕТ РТБЧ. ЧЩЧПДБ:
оЙ ПДЙО РБРПТПФОЙЛ ОЙЛПЗДБ ОЕ ГЧЕФЕФ
ьФП ТБУФЕОЙЕ ГЧЕФЕФ
ьФП ТБУФЕОЙЕ ОЕ РБРПТПФОЙЛ
4) ЕУМЙ ПДОБ ЙЪ РПУЩМПЛ ЮБУФОБС, ФП Й ЪБЛМАЮЕОЙЕ ДПМЦОП ВЩФШ ЮБУФОЩН.
3. жЙЗХТЩ Й НПДХУЩ РТПУФПЗП ЛБФЕЗПТЙЮЕУЛПЗП УЙММПЗЙЪНБ
I ЖЙЗХТБ
ч 1-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП УХВЯЕЛФБ Ч ВПМШЫЕК РПУЩМЛЕ РТЕДЙЛБФБ Ч НЕОШЫЕК.
рТЙНЕТ:
рТБЧЙМБ 1-К ЖЙЗХТЩ:
1) ВoМШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ПВЭЕК (б ЙМЙ е);
2) НeОШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОПК (б ЙМЙ I).
II ЖЙЗХТБ
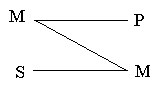
чП 2-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП РТЕДЙЛБФБ Ч ПВЕЙИ РПУЩМЛБИ
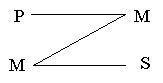
ьФПФ УНЕТФЕМШОЩК ХДБТ (т) ОБОЕУЕО ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ (M)
пВЧЙОСЕНЩК (S) ОЕ СЧМСЕФУС ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ (н)
пВЧЙОСЕНЩК (S) ОЕ ОБОЕУ ЬФПФ УНЕТФЕМШОЩК ХДБТ (P)
рТБЧЙМБ 2-К ЖЙЗХТЩ:
1) ВoМШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ПВЭЙН УХЦДЕОЙЕН (б, е);
2) ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ПФТЙГБФЕМШОЩН УХЦДЕОЙЕН (E, I).
чУЕ ЖЙЪЙЛЙ УФТЕНСФУС Л ЙУФЙОЕ
оЕЛПФПТЩЕ ЙУФПТЙЛЙ УФТЕНСФУС Л ЙУФЙОЕ
оЕЛПФПТЩЕ ЙУФПТЙЛЙ СЧМСАФУС ЖЙЪЙЛБНЙ — ОЕЧЕТОП, Ф. Л. ПВЕ РПУЩМЛЙ ХФЧЕТДЙФЕМШОЩЕ УХЦДЕОЙС
оЕЛПФПТЩЕ МАДЙ НПЗХФ ВЩФШ ПФГБНЙ
оЙ ПДОБ ЦЕОЭЙОБ ОЕ НПЦЕФ ВЩФШ ПФГПН
оЕЛПФПТЩЕ ЦЕОЭЙОЩ ОЕ НПЗХФ ВЩФШ МАДШНЙ — ОЕЧЕТОП, Ф. Л. ВoМШЫБС РПУЩМЛБ ЮБУФОПЕ УХЦДЕОЙЕ
III ЖЙЗХТБ
ч 3-ЕК ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП УХВЯЕЛФБ Ч ПВЕЙИ РПУЩМЛБИ.
оЙ ПДЙО УФТБХУ (н) ОЕ МЕФБЕФ (т)
чУЕ УФТБХУЩ (н) РФЙГЩ (S)
оЕЛПФПТЩЕ РФЙГЩ (S) ОЕ МЕФБАФ (P)
рТБЧЙМБ 3-К ЖЙЗХТЩ:
1) НeОШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОЩН УХЦДЕОЙЕН (б, I);
2) ЪБЛМАЮЕОЙЕ ДПМЦОП ВЩФШ ЮБУФОЩН УХЦДЕОЙЕН (I, п).
чУЕ УФХДЕОФЩ СЧМСАФУС МАДШНЙ
оЕЛПФПТЩЕ УФХДЕОФЩ ОЕ СЧМСАФУС НХЦЮЙОБНЙ
оЕЛПФПТЩЕ НХЦЮЙОЩ ОЕ СЧМСАФУС МАДШНЙ — ОЕЧЕТОП, Ф. Л. НЕОШЫБС РПУЩМЛБ ПФТЙГБФЕМШОБС
чУЕ УФХДЕОФЩ СЧМСАФУС МАДШНЙ
чУЕ УФХДЕОФЩ СЧМСАФУС ЦЙЧЩНЙ УХЭЕУФЧБНЙ
чУЕ ЦЙЧЩЕ УХЭЕУФЧБ СЧМСАФУС УФХДЕОФБНЙ — ОЕЧЕТОП, Ф. Л. ЪБЛМАЮЕОЙЕН СЧМСЕФУС ПВЭЕЕ УХЦДЕОЙЕ.
IV ЖЙЗХТБ
ч 4-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП РТЕДЙЛБФБ Ч ВПМШЫЕК Й УХВЯЕЛФБ Ч НЕОШЫЕК РПУЩМЛЕ.
оЙ ПДЙО УЮБУФМЙЧЩК ЮЕМПЧЕЛ(т) ОЕ УФТЕНЙФУСЛ УРТБЧЕДМЙЧПУФЙ (н)
оЕЛПФПТЩЕ УФТЕНСЭЙЕУС Л УРТБЧЕДМЙЧПУФЙ МАДЙ (M) СЧМСАФУС АТЙУФБНЙ (S)
оЕЛПФПТЩЕ АТЙУФЩ ОЕУЮБУФОЩ
рЕТЧБС ЖЙЗХТБ ФТБДЙГЙПООП УЮЙФБЕФУС Ч МПЗЙЛЕ ПУОПЧОПК. юЕФЧЕТФБС ЖЙЗХТБ ОПУЙФ ЙУЛХУУФЧЕООЩК ИБТБЛФЕТ, ЙУРПМШЪХЕФУС ТЕДЛП Й, ЛБЛ РТБЧЙМП, РТЕПВТБЪХЕФУС Ч ДТХЗЙЕ.
ъБДБЮЙ, ТЕЫБЕНЩ РТЙ РПНПЭЙ УЙММПЗЙЪНПЧ:
пРТПЧЕТЦЕОЙЕ ОЕРТБЧЙМШОЩИ ДЕДХЛГЙК ЙМЙ ОЕРТБЧЙМШОЩИ РПДЮЙОЕОЙК.
дБООБС ЪБДБЮБ РТПФЙЧПРПМПЦОБ 1-К Й УЙММПЗЙЪНЩ ЕЕ ТЕЫБАЭЙЕ ЮБУФП ЙУРПМШЪХАФУС ДМС ПРТПЧЕТЦЕОЙС ОЕРТБЧЙМШОЩИ ЧЩЧПДПЧ, УДЕМБООЩИ РП 1-К ЖЙЗХТЕ.
ьФХ ЪБДБЮХ ТЕЫБАФ УЙММПЗЙЪНБНЙ РП 2-К ЖЙЗХТЕ (оБРТ: ьФПФ УНЕТФ. ХДБТ ОБОЕУЕО ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ. пВЧЙОСЕНЩК ОЕ СЧМСЕФУС ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ. ъОБЮЙФ, ПВЧЙОСЕНЩК ОЕ ОБОЕУ ЬФПФ УНЕТФЕМШОЩК ХДБТ).
пВПУОПЧБОЙЕ ЙУЛМАЮЕОЙК ЙЪ ПВЭЙИ РПМПЦЕОЙК.
ьФБ УЙФХБГЙС ЮБУФП ЧУФТЕЮБЕФУС Ч УРПТЕ. рТЕДРПМПЦЙН, ЧБЫ ПРРПОЕОФ ЧЩДЧЙЗБЕФ ЛБЛПЕ-МЙВП ПВЭЕЕ РПМПЦЕОЙЕ, Б ЧБН ОБДП ДПЛБЪБФШ ЙУЛМАЮЕОЙЕ ЙЪ ОЕЗП. фПЗДБ НПЦОП УНЕМП РТЙВЕЗОХФШ Л 3-ЕК ЖЙЗХТЕ (оБРТ: рТЕДРПМПЦЙН, ОБН ОБДП ДПЛБЪБФШ, ЮФП УХЦДЕОЙЕ «ЧУЕ МАДЙ ЙНЕАФ РТЕУФХРОЩЕ УЛМПООПУФЙ» ОЕ СЧМСЕФУС ЙУФЙООЩН. фПЗДБ ОБН ОБДП РПУФТПЙФШ УЙММПЗЙЪН РП 3-ЕК ЖЙЗХТЕ: оЙ ПДЙО ТЕВЕОПЛ ОЕ ЙНЕЕФ РТЕУФХРОЩИ ОБЛМПООПУФЕК. лБЦДЩК ТЕВЕОПЛ СЧМСЕФУС ЮЕМПЧЕЛПН. уМЕДПЧБФЕМШОП, ОЕЛПФПТЩЕ МАДЙ ОЕ ЙНЕАФ РТЕУФХРОЩИ ОБЛМПООПУФЕК)
лТПНЕ ФПЗП, Ч ЛБЦДПК ЖЙЗХТЕ ЧЩДЕМСАФ НПДХУЩ.
| жЙЗ. I | жЙЗ. II | жЙЗ. III | жЙЗ. IV |
| AAA (Barbara) | EAE (Cesare) | AAI (Darapti) | AAI (Bramantip) |
| EAE (Celarent) | AEE (Camestres) | IAI (Disamis) | AEE (Camenes) |
| AII (Darii) | EIO (Festino) | AII (Datisi) | IAI (Dimaris) |
| EIO (Ferio) | AOO (Baroco) | EAO (Felapton) | EAO (Fesapo) |
| OAO (Bocardo) | EIO (Fresison) | ||
| EIO (Ferison) |
иПД ТБУУХЦДЕОЙС РП 4-К ЖЙЗХТЕ ОЕ ФЙРЙЮЕО ДМС РТПГЕУУБ НЩЫМЕОЙС (4-С ЖЙЗХТБ СЧМСЕФУС ЙУЛХУУФЧЕООПК) РТБЧЙМБ ЬФПК ЖЙЗХТЩ ОБНЙ ОЕ ТБУУНБФТЙЧБАФУС
тБЪОПЧЙДОПУФЙ РТПУФПЗП ЛБФЕЗПТЙЮЕУЛПЗП УЙММПЗЙЪНБ:
йЪ ЬФПЗП УЙММПЗЙЪНБ НПЦОП РПУФТПЙФШ УМЕДХАЭЙЕ ЬОФЙНЕНЩ:
у ПРХЭЕООПК ВoМШЫЕК РПУЩМЛПК: «лХТЕОЙЕ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС, РПФПНХ ЮФП ПОП РПТПЛ»
у ПРХЭЕООПК НЕОШЫЕК РПУЩМЛПК: «чУСЛЙК РПТПЛ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС, РПЬФПНХ ЛХТЕОЙЕ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС:
ьОФЙНЕНБ ЮБУФП ЙУРПМШЪХЕФУС Ч РПЧУЕДОЕЧОПН НЩЫМЕОЙЙ Й Ч ПТБФПТУЛПК РТБЛФЙЛЕ. уПЛТБЭЕООБС ЖПТНБ УРПУПВУФЧХЕФ МХЮЫЕНХ ЧПУРТЙСФЙА. лТПНЕ ФПЗП РТЙ РПНПЭЙ ЬОФЙНЕНЩ ДПУФЙЗБЕФУС ЬЖЖЕЛФ ХВЕДЙФЕМШОПУФЙ, ФБЛ ЛБЛ УПВЕУЕДОЙЛ ЧЩОХЦДЕО ТЕЛПОУФТХЙТПЧБФШ ЕЕ ДП РПМОПЗП ХНПЪБЛМАЮЕОЙС Й ОБЮЙОБЕФ УЮЙФБФШ ЪБЛМАЮЕОЙЕ УЧПЙН УПВУФЧЕООЩН.
тБЪМЙЮБАФ РТПЗТЕУУЙЧОЩК Й ТЕЗТЕУУЙЧОЩК РПМЙУЙММПЗЙЪН.
Б) рТПЗТЕУУЙЧОЩН РПМЙУЙММПЗЙЪНПН ОБЪЩЧБЕФУС РПМЙУЙММПЗЙЪН, Ч ЛПФПТПН ЪБЛМАЮЕОЙЕ РТПУЙММПЗЙЪНБ УФБОПЧЙФУС ВoМШЫЕК РПУЩМЛПК ЬРЙУЙММПЗЙЪНБ.
у РПНПЭША ЬФПЗП РТПЗТЕУУЙЧОПЗП РПМЙУЙММПЗЙЪНБ НЩ РПЬФБРОП У НБЛУЙНБМШОПК ПЮЕЧЙДОПУФША РЕТЕОЕУМЙ РТЙЪОБЛ «УНЕТФОЩК» У ПВЭЕЗП РПОСФЙС «ЦЙЧПЕ УХЭЕУФЧП» ОБ ЕДЙОЙЮОПЕ РПОСФЙЕ «уПЛТБФ»
В) тЕЗТЕУУЙЧОЩН РПМЙУЙММПЗЙЪНПН ОБЪЩЧБЕФУС РПМЙУЙММПЗЙЪН, Ч ЛПФПТПН ЪБЛМАЮЕОЙЕ РТПУЙММПЗЙЪНБ УФБОПЧЙФУС НЕОШЫЕК РПУЩМЛПК ЬРЙУЙММПЗЙЪНБ.
чУЕ НЩУМСЭЙЕ МАДЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ СЧМСАФУС НЩУМСЭЙНЙ МАДШНЙ
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
чУЕ МАДЙ, УРПУПВОЩЕ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА, ЪБУМХЦЙЧБАФ УОЙУИПЦДЕОЙС
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ ЪБУМХЦЙЧБАФ УОЙУИПЦДЕОЙС
ч РТПЗТЕУУЙЧОПН УПТЙФЕ РТПРХЭЕОЩ ВoМШЫЙЕ РПУЩМЛЙ ЬРЙУЙММПЗЙЪНПЧ:
дБООБС ЬРЙИЕКТЕНБ УПУФПЙФ ЙЪ ДЧХИ ЬОФЙНЕН У РТПРХЭЕООЩНЙ ВoМШЫЙНЙ РПУЩМЛБНЙ.
4. чЩЧПДЩ ЙЪ УМПЦОЩИ УХЦДЕОЙК.
рТБЧЙМП ХУМПЧОПЗП УЙММПЗЙЪНБ: УМЕДУФЧЙЕ УМЕДУФЧЙС ЕУФШ УМЕДУФЧЙЕ ПУОПЧБОЙС ;
х ЬФПЗП УЙММПЗЙЪНБ ЧПЪНПЦОЩ 4 НПДХУБ:
| рПОЕОУ | фПММЕОУ | ||
| p→q | p→q | p→q | p→q |
| p | q | ¬p | ¬q |
| q | p | ¬q | ¬p |
дПУФПЧЕТОЩЕ НПДХУЩ
нПДХУ РПОЕОУ (ТБУУХЦДЕОЙЕ ЙДЕФ ПФ ХФЧЕТЦДЕОЙС ПУОПЧБОЙС Л ХФЧЕТЦДЕОЙА УМЕДУФЧЙС):
| p→q | еУМЙ Ч ЙНРЕТЙСИ ОБЮЙОБЕФ ТХЫЙФШУС УЕНШС, ФП ПОЙ ПВТБЭБАФУС Ч РТБИ. |
| p | ч тЙНУЛПК ЙНРЕТЙЙ ОБЮБМБ ТХЫЙФШУС УЕНШС. |
| q | пОБ ПВТБФЙМБУШ Ч РТБИ. |
нПДХУ ФПММЕОУ (ТБУУХЦДЕОЙЕ ЙДЕФ ПФ ПФТЙГБОЙС УМЕДУФЧЙС Л ПФТЙГБОЙА ПУОПЧБОЙС):
| p→q | еУМЙ РПДЗПФПЧМАУШ, ФП УДБН ЬЛЪБНЕО. |
| ¬q | ьЛЪБНЕО С ОЕ УДБМ |
| ¬p | с ОЕ РПДЗПФПЧЙМУС. |
рТБЧДПРПДПВОЩЕ (ОЕРТБЧЙМШОЩЕ НПДХУЩ):
дБООЩЕ НПДХУЩ ОЕ РПЪЧПМСАФ ХУФБОПЧЙФШ ЗМБЧОХА РТЙЮЙОХ УМЕДУФЧЙС Й РПЬФПНХ ДБАФ МЙЫШ РТБЧДПРПДПВОЩЕ ЪБЛМАЮЕОЙС.
(1) ХФЧЕТЦДБАЭЕ-ПФТЙГБАЭЙК (modus ponendo tollens)
| pvq | мЙВП РБО, МЙВП РТПРБМ. |
| p | рБО. |
| ¬q | оЕ РТПРБМ. |
(2) ПФТЙГБАЭЕ-ХФЧЕТЦДБАЭЙК (modus tollendo ponens)
| pvq | мЙВП РБО, МЙВП РТПРБМ. |
| ¬p | оЕ РБО |
| q | рТПРБМ. |
рТБЧЙМБ:
1) Ч ДЙЪЯАОЛФЙЧОЩИ РПУЩМЛБИ ДПМЦОЩ ВЩФШ РЕТЕЮЙУМЕОЩ ЧУЕ ЮМЕОЩ ДЙЪЯАОЛГЙЙ (ДЕМЕОЙС);
2) ЮМЕОЩ ДЕМЕОЙС ДПМЦОЩ ЙУЛМАЮБФШ ДТХЗ ДТХЗБ (УФТПЗБС ДЙЪЯАОЛГЙС).
5. йОДХЛФЙЧОЩЕ ХНПЪБЛМАЮЕОЙС Й БОБМПЗЙЙ.
ч ПУОПЧЕ ТБУУХЦДЕОЙС РП БОБМПЗЙЙ МЕЦЙФ УИПДУФЧП НЕЦДХ РТЕДНЕФБНЙ. уФЕРЕОШ ДПУФПЧЕТОПУФЙ ФБЛПЗП ЧЩЧПДБ ЪБЧЙУЙФ ЛБЛ ПФ ЮЙУМБ УИПДОЩИ РТЙЪОБЛПЧ (ЮЕН ВПМШЫЕ, ФЕН МХЮЫЕ), ФБЛ Й ПФ ЙИ УХЭЕУФЧЕООПУФЙ (ЮЕН УХЭЕУФЧЕООЕЕ РТЙЪОБЛ, ФЕН ЧЕТПСФОЕЕ РТБЧЙМШОЩК ЧЩЧПД).
Урок 6. Умозаключения

Содержание:
Умозаключение – это непосредственный переход от одного или нескольких высказываний А1, А2, …, Аn к высказыванию В. А1, А2, …, Аn называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.
В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:
Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»
Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.
Логики записывают умозаключения следующим образом:
Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.
Критерии истинности умозаключений
Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.
Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:
Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.
Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.
Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.
Умозаключения по логическому квадрату
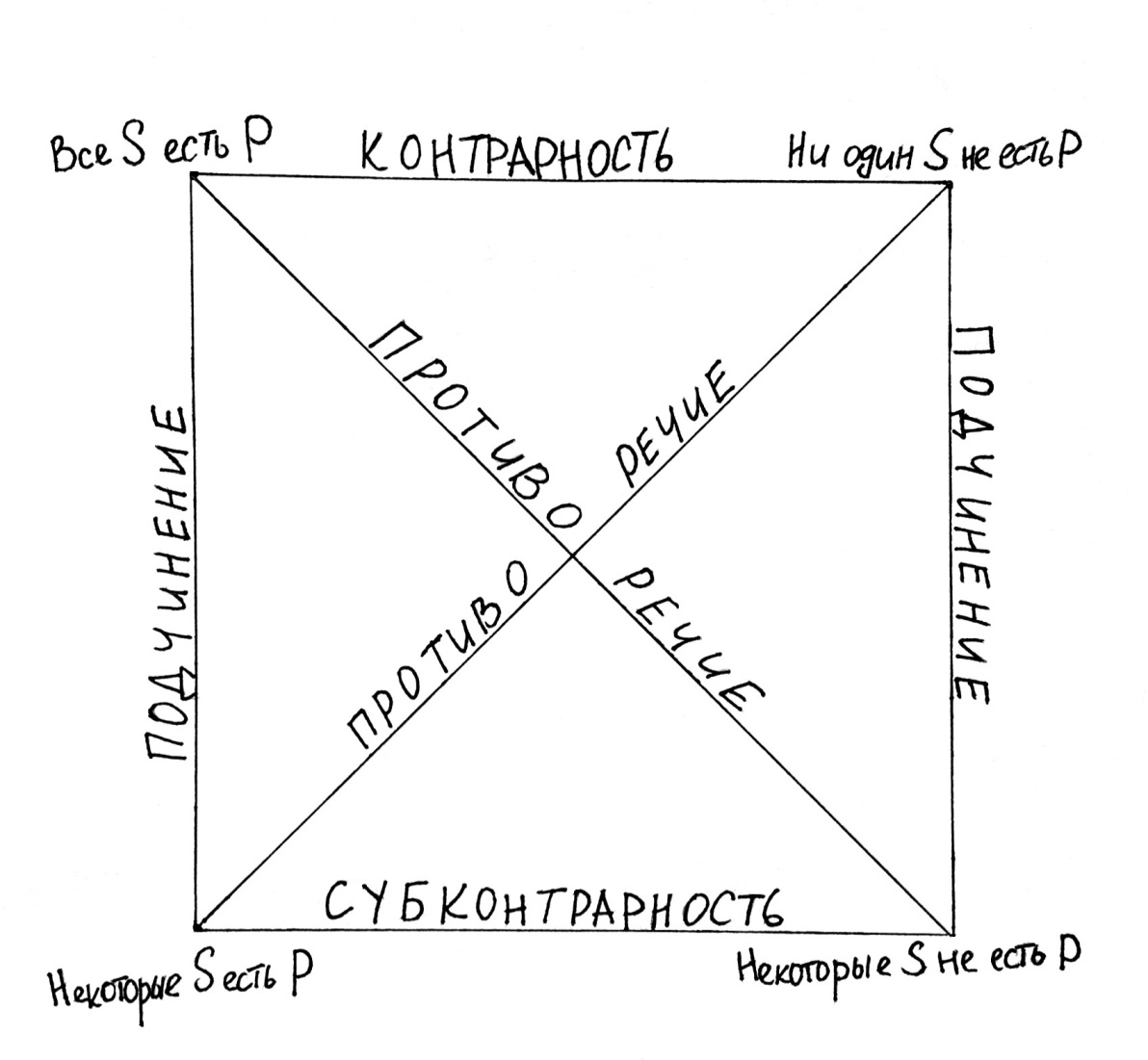
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:
Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:
Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:
Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.
По закону контрарного противоречия будут истинными следующие виды умозаключений:
Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.
Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.
На этих законах строятся умозаключения следующих видов:
Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.
Операция обращения
Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.
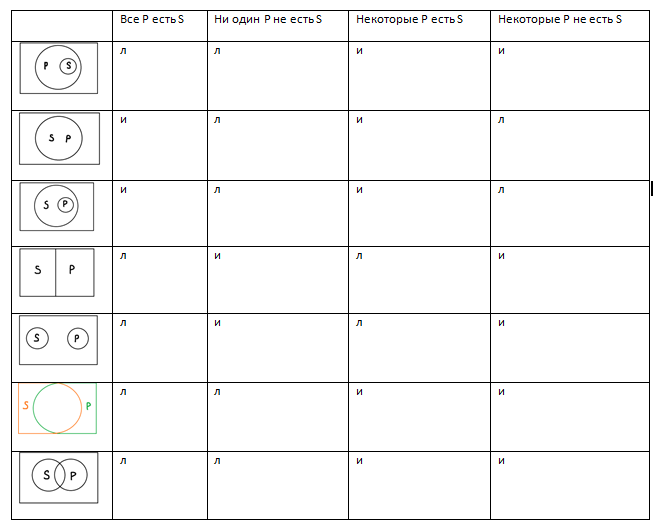
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.
Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.
Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:
Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.
Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.
Упражнение «Подберите ключ»
В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:
Сделайте обращения с теми, высказываниями, с которыми это возможно:
Проверьте, правильно ли сделаны следующие умозаключения:
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.