Что такое эрмитов оператор

Самосопряженный оператор

Структура самосопряженных операторов в бесконечномерных гильбертовых пространствах существенно напоминает конечномерный случай. Другими словами, операторы являются самосопряженными тогда и только тогда, когда они унитарно эквивалентны операторам действительного умножения. С подходящими модификациями этот результат можно распространить на, возможно, неограниченные операторы в бесконечномерных пространствах. Поскольку всюду определенный самосопряженный оператор обязательно ограничен, нужно более внимательно относиться к вопросу о предметной области в неограниченном случае. Это объясняется ниже более подробно.

СОДЕРЖАНИЕ

Ограниченные самосопряженные операторы [ править ]

Свойства ограниченных самосопряженных операторов [ править ]

Симметричные операторы [ править ]

Тонкости неограниченного случая [ править ]

Во многих приложениях мы вынуждены рассматривать неограниченные операторы; примеры включают позиционные, импульсные и гамильтоновы операторы в квантовой механике, а также многие дифференциальные операторы. В неограниченном случае необходимо решить ряд тонких технических проблем. В частности, существует принципиальное различие между операторами, которые просто «симметричны» (определены в этом разделе), и операторами, которые являются «самосопряженными» (определены в следующем разделе). В случае дифференциальных операторов, определенных в ограниченных областях, эти технические вопросы связаны с правильным выбором граничных условий.

Определение симметричного оператора [ править ]

В физической литературе термин « эрмитовский» используется вместо термина «симметричный». В литературе по физике обычно не говорится о различиях между операторами, которые являются просто симметричными, и операторами, которые фактически являются самосопряженными (как определено в следующем разделе).

Хотя понятие симметричного оператора легко понять, это не «правильное» понятие в общем неограниченном случае. В частности, спектральная теорема применима только к самосопряженным операторам (определенным в следующем разделе), а не к большинству операторов, которые являются просто симметричными. В частности, хотя собственные значения симметричного оператора обязательно действительны, симметричный оператор не обязательно должен иметь какие-либо собственные векторы, не говоря уже об их ортонормированном базисе.

В более общем смысле, частично определенный линейный оператор A из топологического векторного пространства E в его непрерывное двойственное пространство E ∗ называется симметричным, если

Простой пример [ править ]

Рассмотрим комплексное гильбертово пространство L 2 [0,1] и дифференциальный оператор

с действительными собственными значениями n 2 π 2 ; хорошо известная ортогональность синусоидальных функций следует как следствие свойства симметрии.

Ниже мы рассмотрим обобщения этого оператора.

Свойства симметричных операторов [ править ]

Самосопряженные операторы [ править ]

Определение самосопряженного оператора [ править ]

Вкратце, плотно определенный линейный оператор A в гильбертовом пространстве является самосопряженным, если он равен своему сопряженному. Иными словами, A является самосопряженным, если (1) область определения A совпадает с областью определения сопряженного, и (2) оператор A согласован со своим сопряженным в этой общей области.

Теперь уточним приведенное выше определение. Для плотно определенного линейного оператора A на H его сопряженный A ∗ определяется следующим образом:

Обратите внимание, что именно плотность области определения оператора, наряду с частью уникальности представления Рисса, обеспечивает правильное определение сопряженного оператора.

Результат типа Хеллингера-Теплица гласит, что оператор, имеющий всюду определенное ограниченное сопряжение, ограничен.

Существенная самосопряженность [ править ]

Геометрическая интерпретация [ править ]

Существует полезный геометрический способ рассмотрения сопряженного оператора A на H следующим образом: мы рассматриваем граф G ( A ) оператора A, определенный формулой

Пример [ править ]

Рассмотрим комплексное гильбертово пространство L 2 ( R ) и оператор, умножающий заданную функцию на x :

Как мы увидим позже, самосопряженные операторы обладают очень важными спектральными свойствами; на самом деле они являются операторами умножения на общих пространствах с мерой.

Различие между симметричными и самосопряженными операторами [ править ]

Как обсуждалось выше, хотя различие между симметричным оператором и самосопряженным (или по существу самосопряженным) оператором является тонким, оно важно, поскольку самосопряженность является гипотезой спектральной теоремы. Здесь мы обсуждаем некоторые конкретные примеры различия; см. ниже раздел о расширениях симметрических операторов для общей теории.

Граничные условия [ править ]

тогда A несимметрична (поскольку граничные члены при интегрировании по частям не обращаются в нуль).

тогда как область определения сопряженного к A равна A ∗ <\displaystyle A^<*>>

С этой областью A по существу самосопряжен. [9]

Операторы Шредингера с сингулярными потенциалами [ править ]

В этом случае, если мы сначала определим на пространстве гладких, быстро убывающих функций, сопряженный будет «тот же» оператор (т. Е. Заданный той же формулой), но в максимально возможной области, а именно H ^ <\displaystyle <\hat >>

Условия, при которых операторы Шредингера являются самосопряженными или существенно самосопряженными, можно найти в различных учебниках, таких как книги Березина и Шубина, Холла, Рида и Саймона, перечисленные в ссылках.

Спектральная теорема [ править ]

Спектральная теорема в целом может быть выражена аналогично возможности «диагонализации» оператора, показывая, что он унитарно эквивалентен оператору умножения. Другие версии спектральной теоремы аналогичным образом предназначены для улавливания идеи о том, что самосопряженный оператор может иметь «собственные векторы», которые на самом деле не находятся в рассматриваемом гильбертовом пространстве.

Формулировка спектральной теоремы [ править ]

Один из вариантов спектральной теоремы можно сформулировать следующим образом.

Теорема. Любой оператор умножения является (плотно определенным) самосопряженным оператором. Любой самосопряженный оператор унитарно эквивалентен оператору умножения. [13]

Другие версии спектральной теоремы можно найти в указанной выше статье о спектральных теоремах.

Функциональное исчисление [ править ]

который является оператором, определяющим эволюцию во времени в квантовой механике.

Разрешение личности [ править ]

Принято вводить следующие обозначения

Приведенное выше определение операторного интеграла можно свести к определению скалярнозначного интеграла Стилтьеса с использованием слабой операторной топологии. Однако в более современных методах лечения этого представления обычно избегают, поскольку с большинством технических проблем можно справиться с помощью функционального исчисления.

Формулировки в физической литературе [ править ]

В физике, особенно в квантовой механике, спектральная теорема выражается способом, который объединяет спектральную теорему, как указано выше, и функциональное исчисление Бореля с использованием обозначений Дирака следующим образом:

f ( H ) = ∫ d E | Ψ E ⟩ f ( E ) ⟨ Ψ E | <\displaystyle f(H)=\int dE\left|\Psi _\rangle f(E)\langle \Psi _\right|>

I = ∫ d E | Ψ E ⟩ ⟨ Ψ E | <\displaystyle I=\int dE\left|\Psi _\right\rangle \left\langle \Psi _\right|>

H eff ∗ | Ψ E ∗ ⟩ = E ∗ | Ψ E ∗ ⟩ <\displaystyle H_<\text>^<*>\left|\Psi _^<*>\right\rangle =E^<*>\left|\Psi _^<*>\right\rangle >

и запишем спектральную теорему как:

f ( H eff ) = ∫ d E | Ψ E ⟩ f ( E ) ⟨ Ψ E ∗ | <\displaystyle f\left(H_<\text>\right)=\int dE\left|\Psi _\right\rangle f(E)\left\langle \Psi _^<*>\right|>

(См. Контекст, в котором такие операторы появляются в теории рассеяния, в методе разбиения Фешбаха – Фано ).

Расширения симметричных операторов [ править ]

В нескольких контекстах возникает следующий вопрос: если оператор A в гильбертовом пространстве H симметричен, когда он имеет самосопряженные расширения? Оператор, имеющий единственное самосопряженное расширение, называется по существу самосопряженным ; эквивалентно, оператор является по существу самосопряженным, если его замыкание (оператор, график которого является замыканием графика A ) самосопряженный. В общем, симметричный оператор может иметь много самосопряженных расширений или вообще не иметь. Таким образом, нам нужна классификация его самосопряженных расширений.

Первый основной критерий существенной самосопряженности следующий: [15]

Оператор S ( U ) плотно определен и симметричен.

Отображения W и S обратны друг другу. [ требуется разъяснение ]

Это сразу дает нам необходимое и достаточное условие для того, чтобы A имела самосопряженное расширение, а именно:

Мы видим, что существует биекция между симметричными расширениями оператора и изометрическими расширениями его преобразования Кэли. Симметричное расширение самосопряжено тогда и только тогда, когда соответствующее изометрическое расширение унитарно.

Самосопряженные расширения в квантовой механике [ править ]

Пример. Самосопряженного оператора импульса p для частицы, движущейся по полупрямой, не существует. Тем не менее гамильтониан «свободной» частицы на полупрямой имеет несколько самосопряженных расширений, соответствующих различным типам граничных условий. Физически эти граничные условия связаны с отражениями частицы в начале координат (см. Рид и Саймон, том 2). p 2 <\displaystyle p^<2>>

Формулы фон Неймана [ править ]

Предположим, что A симметрично плотно определено. Тогда любое симметрическое расширение A является ограничением A *. Действительно, если A ⊆ B и B симметрично, то B ⊆ A *, применяя определение dom ( A *).

Они упоминаются как формулы фон Неймана в справочнике Ахиезера и Глазмана.

Примеры [ править ]

Симметричный оператор, который не является самосопряженным [ править ]

на пространстве непрерывно дифференцируемых комплекснозначных функций на [0,1], удовлетворяющих граничным условиям

− i u ′ = i u − i u ′ = − i u <\displaystyle <\begin-iu’&=iu\\-iu’&=-iu\end>>

Операторы с постоянными коэффициентами [ править ]

P ( x → ) = ∑ α c α x α <\displaystyle P\left(<\vec >\right)=\sum _<\alpha >c_<\alpha >x^<\alpha >>

Мы также используем обозначения

Тогда оператор P (D), определенный на пространстве бесконечно дифференцируемых функций с компактным носителем на R n формулой

существенно самосопряжен на L 2 ( R n ).

P ϕ ( x ) = ∑ α a α ( x ) [ D α ϕ ] ( x ) <\displaystyle P\phi (x)=\sum _<\alpha >a_<\alpha >(x)\left[D^<\alpha >\phi \right](x)>

Соответствующему P есть другой дифференциальный оператор, формальный сопряженный к P

Теория спектральной множественности [ править ]

Равномерная множественность [ править ]

Сначала определим равномерную кратность :

Неотрицательные счетно-аддитивные меры μ, ν взаимно сингулярны тогда и только тогда, когда они поддерживаются на непересекающихся борелевских множествах.

Это представление уникально в следующем смысле: для любых двух таких представлений одного и того же A соответствующие меры эквивалентны в том смысле, что они имеют одинаковые множества меры 0.

Прямые интегралы [ править ]

Теорема спектральной кратности может быть переформулирована на языке прямых интегралов гильбертовых пространств:

Теперь мы можем сформулировать результат классификации самосопряженных операторов: два самосопряженных оператора унитарно эквивалентны тогда и только тогда, когда (1) их спектры совпадают как множества, (2) меры, появляющиеся в их представлениях прямого интеграла, имеют одинаковые множества меры нуль и (3) их функции спектральной кратности почти всюду совпадают относительно меры в прямом интеграле. [21]

Пример: структура лапласиана [ править ]

Как отмечалось выше, лапласиан диагонализуется преобразованием Фурье. На самом деле более естественно рассматривать отрицание лапласиана −∆, поскольку как оператор он неотрицателен; (см. эллиптический оператор ).

Чистый точечный спектр [ править ]

Этот гамильтониан имеет чисто точечный спектр; это типично для гамильтонианов связанных состояний в квантовой механике. Как было указано в предыдущем примере, достаточным условием наличия у неограниченного симметричного оператора собственных векторов, образующих базис гильбертова пространства, является наличие у него компактного обратного.

Источник

Самосопряженный оператор

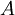
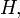
Эрмитов (самосопряжённый) оператор — оператор в комплексном гильбертовом пространстве удовлетворяющий равенству , где (х, у) — скалярное произведение в H.

Спектр (множество собственных чисел) самосопряжённого оператора является вещественным.

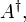
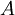
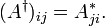
В конечномерных пространствах матрица самосопряжённого оператора является эрмитовой. Матрицей, эрмитово сопряжённой к данной, называют матрицу получаемую из исходной матрицы путем её транспонирования и перехода к комплексно сопряжённой, то есть Матрицу, равную своему эрмитовому сопряжению, называют эрмитовой, или самосопряжённой:

Собственные числа эрмитовой матрицы вещественны. У неё всегда существует ортонормированный базис из собственных векторов, собственные векторы, соответствующие различным собственным значениям, ортогональны.

Название дано в честь Шарля Эрмита, французского математика.

Эрмитовы операторы играют важную роль в квантовой механике, где с их помощью представляют наблюдаемые физические величины, см. Принцип неопределённости Гейзенберга.

См. также

Полезное

Смотреть что такое «Самосопряженный оператор» в других словарях:

САМОСОПРЯЖЕННЫЙ ОПЕРАТОР — см. Эрмитов оператор. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

САМОСОПРЯЖЕННЫЙ ОПЕРАТОР — э р м и т о в о п е р а т о р, линейный оператор А, определенный на линейном всюду плотном множестве D(А)гильбертова пространства Ни совпадающий со своим сопряженным оператором А, т … Математическая энциклопедия

НЕСАМОСОПРЯЖЕННЫЙ ОПЕРАТОР — линейный оператор в гильбертовом пространстве, спектральный анализ которого не укладывается в рамки теории самосопряженных операторов и ее простейших обобщений: теории унитарных операторов и теории нормальных операторов. Н. о. возникают при… … Математическая энциклопедия

ПОЛОЖИТЕЛЬНЫЙ ОПЕРАТОР — положительное отображение, 1) П. о. в гильбертовом пространстве линейный оператор А, для к рого соответствующая квадратичная форма ( Ах, х).неотрицательна. П. о. необходимо симметричен и допускает самосопряженное расширение, также являющееся П. о … Математическая энциклопедия

ИЗОМЕТРИЧЕСКИЙ ОПЕРАТОР — отображение Uметрич. пространства (X,rX). в метрич. пространство (Y, rY). такое, что для любых Если Xи Y действительные линейные нормированные пространства, U(X)=Y и U(0)=0, то U линейный оператор. И. о. Uотображает Xна U(X)взаимно однозначно,… … Математическая энциклопедия

ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия

Положительный оператор — Термин Положительный оператор в Теории операторов употребляется в двух различных смыслах. Под положительным оператором между векторными решетками понимают линейный оператор, переводящий положительные вектора в положительные. Самосопряженный… … Википедия

Источник

Эрмитов оператор

Смотреть что такое «Эрмитов оператор» в других словарях:

ЭРМИТОВ ОПЕРАТОР — линейный оператор А в гильбертовом пространстве Н сплотной областью определения D(A )и такой, что = для любых х, у D(A). Это условие эквивалентно тому, что: 1) D(A) D(A*), 2) Ах = А * х для всех х D(A), где А * … Физическая энциклопедия

эрмитов оператор — ermitinis operatorius statusas T sritis fizika atitikmenys: angl. Hermitian operator; selfadjoint operator vok. Hermite Operator, m; hermitescher Operator, m; selbstadjungierter Operator, m rus. самосопряжённый оператор, m; эрмитов оператор, m… … Fizikos terminų žodynas

Оператор плотности — Матрица плотности (оператор плотности) один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в равной мере может задавать как чистые, так … Википедия

Оператор координаты — В квантовой физике наряду с оператором импульса имеет место оператор координаты. Так как координата является вещественной величиной, то оператор координаты эрмитов. Содержание 1 Определение 2 Свойства 3 … Википедия

ЛИНЕЙНЫЙ ОПЕРАТОР — А в векторном пространстве L отображение, сопоставляющее каждому вектору е век poro множества D (содержащегося в L и наз. областью определения Л. о.) др. вектор, обозначаемый Ае (и называемый значением Л. о. на векторе е). Выполнены след. условия … Физическая энциклопедия

Сопряжённый оператор — Содержание 1 Общее линейное пространство 2 Топологическое линейное пространство … Википедия

САМОСОПРЯЖЕННЫЙ ОПЕРАТОР — см. Эрмитов оператор. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

самосопряжённый оператор — ermitinis operatorius statusas T sritis fizika atitikmenys: angl. Hermitian operator; selfadjoint operator vok. Hermite Operator, m; hermitescher Operator, m; selbstadjungierter Operator, m rus. самосопряжённый оператор, m; эрмитов оператор, m… … Fizikos terminų žodynas

Источник

Эрмитовы операторы

Эрмитовы операторы

Содержание

Пусть M и N — линейные множества. Оператор L, преобразующий элементы множества M в элементы множества N, называется линейным, если для любых элементов f и g из M и комплексных чисел λ и μ справедливо равенство

При этом множество M = M_L называется областью определения оператора L. Если Lf = f при всех f Є M, то оператор L называется тождественным (единичным) оператором. Единичный оператор будем обозначать через I.

Пусть L — линейный оператор с областью определения M_L . Уравнение

называется линейным неоднородным уравнением. В уравнении (2) заданный элемент F называется свободным членом (или правой частью), а неизвестный элемент и из M_L — решением этого уравнения.

Если в уравнении (2) свободный член F положить равным нулю, то полученное уравнение

называется линейным однородным уравнением, соответствующим уравнению (2).

В силу линейности оператора L совокупность решений однородного уравнения (3) образует линейное множество; в частности, и = 0 всегда является решением этого уравнения.

Всякое решение и линейного неоднородного уравнения (2) (если оно существует) представляется в виде суммы частного решения и_о этого уравнения и общего решения ŭ, соответствующего линейного однородного уравнения (3)

Рассмотрим линейное однородное уравнение

где λ — комплексный параметр. Это уравнение имеет нулевое решение при всех λ. Может случиться, что при некоторых λ оно имеет ненулевые решения из M_L. Те комплексные значения λ, при которых уравнение (5) имеет ненулевые решения из M_L, называются собственными значениями оператора L, а соответствующие решения — собственными элементами (функциями), соответствующими этому собственному значению. Полное число r, 1 ≤ r ≤ ∞, линейно независимых собственных элементов, соответствующих данному собственному значению λ, называется кратностью этого собственного значения; если кратность r = 1, то λ называется простым собственным значением.

Если кратность r собственного значения λ оператора L конечна и u₁. и₂ — соответствующие линейно независимые собственные элементы, то любая их линейная комбинация

также является собственным элементом, соответствующим этому собственному значению, и приведенная формула дает общее решение уравнения (5). Отсюда вытекает: если решение уравнения

существует, то его общее решение представляется формулой

где и* — частное решение (6) и с_k, k = l,2. r, — произвольные постоянные.

Для того чтобы линейный оператор L был эрмитовым, необходимо и достаточно, чтобы порожденная им квадратичная форма (Lf, f), f Є M_l, где M_l плотна в L₂(G), принимала только вещественные значения.

В частности, всякий положительный оператор эрмитов.

Теорема. Если оператор L эрмитов (положительный), то все его собственные значения вещественны (неотрицательны), а собственные функции, соответствующие различным собственным значениям, ортогональны.

Доказательство. Пусть λ₀ — собственное значение, u₀ — соответствующая нормированная собственная функция эрмитова оператора L, L u₀ = λ₀u₀. Умножая скалярно это равенство на u₀, получим

Но для эрмитова (положительного) оператора квадратичная форма (Lf, f) принимает только вещественные (неотрицательные) значения, и, стало быть, в силу (7) λ₀ — вещественное (неотрицательное) число.

Докажем, что любые собственные функции и₁ и и₂, соответствующие различным собственным значениям λ₁ и λ₂, ортогональны. Действительно, из соотношений

из вещественности λ₁ и λ₂ и из эрмитовости оператора L получаем цепочку равенств

Предположим, что множество собственных значений эрмитова оператора L не более чем счетно, а каждое собственное значение конечной кратности. Перенумеруем все его собственные значения: λ₁,λ₂. повтори λ_k столько раз, какова его кратность. Соответствующие собственные функции обозначим через и₁,и₂,… так, чтобы каждому собственному значению соответствовала только одна собственная функция и_k:

Собственные функции, соответствующие одному и тому же собственному значению, можно выбрать ортонормальными, используя процесс ортогонализации Шмидта. Всякая ортонормальная система <φ_k> состоит из линейно независимых функций. Всякая система ψ₁,ψ₂. линейно независимых функций из L₂(G) преобразуется в ортонормальную систему φ₁,φ₂, — следующим процессом ортогонализации Шмидта:

При этом опять получаются собственные функции, соответствующие тому же самому собственному значению. По доказанной теореме собственные функции, соответствующие различным собственным значениям, ортогональны.

Таким образом, если система собственных функций <и_к> эрмитова оператора L не более чем счетна, то ее можно выбрать ортонормальной:

Список литературы

1. Владимиров B.C., Жаринов В. В. Уравнения математической физики: Учебник для вузов. — М.: Физмат-лит, 2000.

2. Владимиров В. С. Уравнения математической физики. — Изд. 5-е. — М.: Наука, 1985.

3. Никольский СМ. Математический анализ.—Изд. 5-е. — М.: Физмат-лит, 2000.

Источник