делители нуля в кольце вычетов
Кольца, тела, поля
Определение 2.5. Кольцом называют алгебру сигнатура которой состоит из двух бинарных и двух нульарных операций, причем для любых выполняются равенства:
Операцию называют сложением кольца, операцию умножением кольца, элемент — нулем кольца, элемент — единицей кольца.
Равенства 1–7, указанные в определении, называют аксиомами кольца. Рассмотрим эти равенства с точки зрения понятия группы и моноида.
Связь между сложением кольца и умножением кольца устанавливает аксиома 7, согласно которой операция умножения дистрибутивна относительно операции сложения.
Замечание 2.2. В литературе встречается иной состав аксиом кольца, относящихся к умножению. Так, могут отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не ассоциативно). В этом случае выделяют ассоциативные кольца (к аксиомам кольца добавляют требование ассоциативности умножения) и кольца с единицей. В последнем случае добавляются требования ассоциативности умножения и существования единицы.
Определение 2.6. Кольцо называют коммутативным, если его операция умножения коммутативна.
Пример 2.12. а. Алгебра есть коммутативное кольцо. Отметим, что алгебра кольцом не будет, поскольку — коммутативный моноид, но не группа.
в. Алгебра — коммутативное кольцо, что следует из свойств пересечения и симметрической разности множеств.
г. Пример некоммутативного кольца дает множество всех квадратных матриц фиксированного порядка с операциями сложения и умножения матриц. Единицей этого кольца является единичная матрица, а нулем — нулевая.
д. Пусть — линейное пространство. Рассмотрим множество всех линейных операторов, действующих в этом пространстве.
Основные аксиомы и тождества кольца
Аксиомы кольца называют также основными тождествами кольца. Тождество кольца — это равенство, справедливость которого сохраняется при подстановке вместо фигурирующих в нем переменных любых элементов кольца. Основные тождества постулируются, и из них затем могут быть выведены как следствия другие тождества. Рассмотрим некоторые из них.
Напомним, что аддитивная группа кольца коммутативна и в ней определена операция вычитания.
Теорема 2.8. В любом кольце выполняются следующие тождества:
Докажем третью пару тождеств. Рассмотрим первое из них. С учетом доказанного выше имеем
т.е. тождество справедливо. Второе тождество этой пары доказывается аналогично.
Первые два тождества из доказанных в теореме 2.8 выражают свойство, называемое аннулирующим свойством нуля в кольце. Третья же пара тождеств указанной теоремы выражает свойство дистрибутивности операции умножения кольца относительно операции вычитания. Таким образом, производя вычисления в любом кольце, можно раскрывать скобки и менять знаки так же, как и при сложении, вычитании и умножении действительных чисел.
Кольца и делители нуля
При отличных от нуля и приведенные матрицы являются делителями нуля.
Если в кольце имеются делители нуля, то подмножество всех ненулевых элементов кольца не образует группы по умножению уже хотя бы потому, что это подмножество не замкнуто относительно операции умножения, т.е. существуют ненулевые элементы, произведение которых равно нулю.
Кольцо, в котором множество всех ненулевых элементов по умножению образует группу, называют телом, коммутативное тело — полем, а группу ненулевых элементов тела (поля) по умножению — мультипликативной группой этого тела (поля). Согласно определению, поле есть частный случай кольца, в котором операции обладают дополнительными свойствами. Выпишем все свойства, выполнение которых требуется для операций поля. Их еще называют аксиомами поля.
б. Алгебры и есть поля, называемые полями действительных и комплексных чисел соответственно.
в. Примером тела, не являющегося полем, может служить алгебра кватернион.
Итак, мы видим, что известным законам сложения и умножения чисел соответствуют аксиомы поля. Занимаясь числовыми расчетами, мы «работаем в полях», а именно имеем дело преимущественно с полями рациональных и вещественных чисел, иногда «переселяемся» в поле комплексных чисел.
Делители нуля
В абстрактной алгебре, ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.
Правый делитель нуля определяется аналогично: ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.
Элемент, который является и правым и левым делителем нуля одновременно называется делителем нуля. Если умножение в кольце коммутативно тогда правые и левые делители совпадают. Ненулевые элементы кольца, которые не являются ни правыми, ни левыми делителями нуля называются обычными элементами.
Пример: в кольце 
Ассоциативное и коммутативное кольцо с единицей 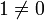
Внешние ссылки
Смотреть что такое «Делители нуля» в других словарях:
Делитель нуля — В абстрактной алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0. Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0 … Википедия
АЛГЕБРА АБСТРАКТНАЯ — (общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых… … Энциклопедия Кольера
ДВОЙНЫЕ И ДУАЛЬНЫЕ ЧИСЛА — гиперкомплексные числа вида a+bе, где аи b действительные числа, и для двойных чисел е 2= + 1, а для дуальных чисел е 2=0. Сложение Д. и д. ч. определяется формулой Умножение двойных чисел производится по формуле а дуальных чисел по формуле… … Математическая энциклопедия
Двойные числа — О гиперкомплексных числах параболического типа см. дуальные числа Двойные числа или паракомплексные числа, расщепляемые комплексные числа, комплексные числа гиперболического типа гиперкомплексные числа вида « », где и вещественные… … Википедия
Процедура Кэли — Диксона (процедура удвоения) это рекурсивная процедура построения алгебр над полем вещественных чисел, с удвоением размерности на каждом шагу. Названа в честь Артура Кэли и Леонарда Диксона. Эта процедура позволяет построить комплексные числа,… … Википедия
АЛЬТЕРНАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — Альтернативным кольцом (А. к.) наз. кольцо, в к ром каждые два элемента порождают ассоциативное подкольцо; альтернативной алгеброй (А. а.) наз. линейная алгебра, являющаяся А. к. Согласно теореме Артина класс всех А. к. задается системой тождеств … Математическая энциклопедия
АССОЦИАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — кольца и алгебры с ассоциативным умножением, т. е. множества с двумя бинарными операциями сложением + и умножением Х, являющиеся абелевой группой по сложению и полугруппой по умножению, причем умножение дистрибутивно (слева и справа) относительно … Математическая энциклопедия
ВИТТА КОЛЬЦО — поля k, кольцо типов квадратичных форм над k, кольцо W(k).классов невырожденных квадратичных форм на конечномерных векторных пространствах над kпо следующему отношению эквивалентности: форма f1 эквивалентна форме тогда и только тогда, когда для… … Математическая энциклопедия
ГРУППОВАЯ АЛГЕБРА — группы G над полем K ассоциативная алгебра над полем К, элементами к рой являются всевозможные формальные конечные суммы вида а операции определяются формулами: (в правой части второй формулы сумма также конечна). Эта алгебра обозначается… … Математическая энциклопедия
Делители нуля в кольце вычетов
В кольцах целых, рациональных и действительных чисел из того, что произведение ab =0, следует, что либо а=0, либо b =0. Но в кольце квадратных матриц порядка n >1 это свойство уже не выполняется, так как, например,



2. Рассмотрим множество пар целых чисел (а, b ), в котором заданы операции сложения и умножения:
Это множество образует коммутативное кольцо с единицей (1,1) и делителями нуля, так как (1,0)(0,1)=(0,0).
Если в кольце нет делителей нуля, то в нем выполняется закон сокращения, т. е. ab = ac , а 




Обратимый элемент не может быть делителем нуля, так как. если ab =0, то a -1 ( ab ) =0 



Теорема. Все обратимые элементы кольца К с единицей образуют группу относительно умножения.
Важную алгебраическую структуру образуют коммутативные кольца К, в которых каждый ненулевой элемент обратим,, т. е. относительно операции умножения множество K \ <0>образует группу. В таких кольцах определены три операции: сложение, умножение и деление.
Коммутативное кольцо Р с единицей 1 
Относительно умножения все отличные от нуля элементы поля образуют группу, которая называется мультипликативной группой поля.


Докажем, например, второе из них. Пусть х= 




1. Кольцо целых чисел не образует поля. Полем является множество рациональных и множество действительных чисел.
Кольцо вычетов



Целые числа a,b сравнимы по модулю n, если при делении на число n эти числа дают один остаток (a mod n = b mod n).
При делении на n возможные значения остатка 0,1,…,n-1.
Обозначим [k] – класс сравнимых между собой чисел, дающих при делении на n остаток k. Например, для n=4 образуется четыре класса:
Таким образом, при делении на n образуется n классов [0],[1],…,[n-1]. Эти классы называются классами вычетов по модулю n. Множество Zn=<[0],[1],…, [n-1]> называется полной системой вычетов. В дальнейшем квадратные скобки будем опускать Zn=<0,1,…,n-1>.
Число из класса [a] имеет вид in+a. Выясним, в какой класс попадет сумма чисел из классов [a],[b]:
Это число при делении на n дает остаток ((i+j)n+(a+b)) mod n = (a+b) mod n. Таким образом, сумма любых двух чисел из классов [a],[b] принадлежит классу [(a+b) mod n]. В соответствии с этим на множестве Zn введем операцию сложения:
В этом соотношении слева используется алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции сложения:
· операция коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция сложения в правой части соотношения a+b=(a+b) mod n.
· элемент, противоположный элементу a, определяется следующим образом —a=n—a, т.к. a+(—a)=(—a)+a=(a+n—a) mod n =0.
Таким образом, алгебра A= образует абелевую группу относительно операции сложения.
Теперь выясним, в какой класс попадет произведение чисел из классов [a],[b]:
Это число при делении на n дает остаток (ab) mod n.
Поэтому операция умножения на множестве Zn определяется как:
В этом соотношении слева – алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции умножения:
· операция умножения коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция умножения в правой части соотношения a*b=(ab) mod n.
Такую алгебру называют кольцом вычетов.
Кроме того, в кольце вычетов выполняется условие коммутативности умножения, следовательно, данная алгебра является коммутативным кольцом.
Если n – составное, то кольцо вычетов содержит делители нуля. Действительно, если n=kl, тогда по определению умножения k*l=(kl) mod n =0.
Результаты операций сложения умножения и вычитания в A= представлены в табл.1.2-1.4 соответственно. Делителями нуля является пара элементов a=2,b=2.
9.Сравнения. Кольцо классов вычетов. Делители нуля.
Решаем четыре системы сравнений 7 страница
3. (для кольца с единицей);
Определение 2. Два ненулевых элемента кольца, произведение которых равно нулю, называются делителями нуля кольца.
Если кольцо не имеет делителей нуля, то в нем справедливы т.н. законы сокращения:
Определение 3. Коммутативное кольцо с единицей и без делителей нуля называется областью целостности, или целостным кольцом.
Определение 17. Целостное кольцо, в котором каждый ненулевой элемент обратим, называется
Пример 10. – поле рациональных чисел.
Пример 11. – вещественное «квадратичное» поле.
Пример 13. – поле гауссовых чисел.
Конечно, полями являются и множества вещественных и комплексных чисел относительно стандартных операций сложения и умножения, заданных в них.
Лемма 1.Если кольцо с единицей и без делителей нуля имеет положительную
характеристику, то эта характеристика есть простое число.
Следствие. Положительная характеристика поля есть простое число. В частности, характеристика конечного поля есть простое число
Пример 14. Поле из примера 12 имеет характеристику, равную р.
Теорема1. Пусть – коммутативное кольцо простой характеристики р. Тогда
Пример 15. Четные числа образуют подкольцо в кольце всех целых чисел.
Пример 16. Диагональные матрицы образуют подкольцо в кольце квадратных матриц.
Теорема2. Непустое подмножество кольца является подкольцом в нем тогда и только тогда, когда выполнены условия:
Заметим, что подкольцо наследует не все свойства родительского кольца. Это хорошо видно на примерах 1 и 6.
Пример 17. Подкольцо четных чисел есть идеал в кольце всех целых чисел. По аналогии, числа кратные некоторому также образуют идеал в этом кольце.
Учитывая эти свойства нетрудно непосредственно показать, что следующие операции над классами корректны:
Дадим еще несколько определений. Пусть – коммутативное кольцо с единицей.
Определение 9. Делители единицы называются обратимыми элементами кольца.
Определение 12. Идеал кольца называется простым идеалом, если для
Определение 14. Целостное кольцо называется кольцом главных идеалов, если каждый идеал кольца является главным, т.е. существует элемент такой, что
Теорема 4. Пусть – коммутативное кольцо с единицей. Тогда
(i) Идеал M кольца R является максимальным тогда и только тогда, когда факторкольцо
(ii) Идеал P кольца R является простым тогда и только тогда, когда факторкольцо
является целостным кольцом.
(iii) Каждый максимальный идеал кольца R является простым.
Пример 22. – кольцо главных идеалов. Это легко показать, используя теорему о делении с остатком. В этом кольце роль простых элементов играют простые числа, правда, «со знаком». Отсюда получается еще одно доказательство, что кольцо классов вычетов по простому модулю есть поле.
Пример 24. Покажите, что – кольцо целых гауссовых чисел есть кольцо главных идеалов. Укажите простые элементы в этом кольце.
Определение 16. Поле называется простым, если не имеет собственных (т.е. отличных от него самого) подполей.
Пример 27. Поле рациональных чисел есть простое поле. Оно является подполем любого числового поля.
Пример 29. Поле является простым. Проверьте это.
Раздел девятнадцатый
Расширения полей. Простое расширение. Конечное расширение. Алгебраичность.
Надо отметить, что понятия алгебраичности и трансцендентности относительны, т.е. прямо связаны с полем, над которым рассматриваются.
Этим свойством и условием нормированности многочлен определен однозначно.
Определение 20. Пусть есть алгебраический над полем элемент. Тогда степень его
Следствие. Пересечение всех подполей данного поля является простым полем. Это поле называют простым подполем этого поля.
Кольцо вычетов
Целые числа a,b сравнимы по модулю n, если при делении на число n эти числа дают один остаток (a mod n = b mod n).
При делении на n возможные значения остатка 0,1,…,n-1.
Обозначим [k] – класс сравнимых между собой чисел, дающих при делении на n остаток k. Например, для n=4 образуется четыре класса:
Таким образом, при делении на n образуется n классов [0],[1],…,[n-1]. Эти классы называются классами вычетов по модулю n. Множество Zn=<[0],[1],…, [n-1]> называется полной системой вычетов. В дальнейшем квадратные скобки будем опускать Zn=<0,1,…,n-1>.
Число из класса [a] имеет вид in+a. Выясним, в какой класс попадет сумма чисел из классов [a],[b]:
Это число при делении на n дает остаток ((i+j)n+(a+b)) mod n = (a+b) mod n. Таким образом, сумма любых двух чисел из классов [a],[b] принадлежит классу [(a+b) mod n]. В соответствии с этим на множестве Zn введем операцию сложения:
В этом соотношении слева используется алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции сложения:
· операция коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция сложения в правой части соотношения a+b=(a+b) mod n.
· элемент, противоположный элементу a, определяется следующим образом —a=n—a, т.к. a+(—a)=(—a)+a=(a+n—a) mod n =0.
Таким образом, алгебра A= образует абелевую группу относительно операции сложения.
Теперь выясним, в какой класс попадет произведение чисел из классов [a],[b]:
Это число при делении на n дает остаток (ab) mod n.
Поэтому операция умножения на множестве Zn определяется как:
В этом соотношении слева – алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции умножения:
· операция умножения коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция умножения в правой части соотношения a*b=(ab) mod n.
Итак, алгебра A= образует абелевую группу относительно операции сложения, является полугруппой относительно умножения (умножение ассоциативно), и умножение дистрибутивно относительно сложения, следовательно, алгебра A — кольцо.
Такую алгебру называют кольцом вычетов.
Кроме того, в кольце вычетов выполняется условие коммутативности умножения, следовательно, данная алгебра является коммутативным кольцом.
Если n – составное, то кольцо вычетов содержит делители нуля. Действительно, если n=kl, тогда по определению умножения k*l=(kl) mod n =0.
Результаты операций сложения умножения и вычитания в A= представлены в табл.1.2-1.4 соответственно. Делителями нуля является пара элементов a=2,b=2.
Не нашли то, что искали? Воспользуйтесь поиском:
Выписать все делители нуля в кольце классов вычетов по модулю 6

Вариант №1.
1082x1983+632x411+197x292+1410(mod11). Вариант №2.
368x663+1354x732+104x671+3430(mod11). Вариант №3.
а) Выписать все делители нуля в кольце классов вычетов по модулю 9.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №4.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №5.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №8.
304x622+359x433+191x81+264x231+1380(mod7). Вариант №9.
1082x1983+632x411+430x1832+197x292+1410(mod11). Вариант №10.
368x663+1354x732+890x1342+104x671+3430(mod11). Вариант №11.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №12.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №13.
63x708+35x319+426x602+947x394+37x2325+680(mod5). Вариант №14.
213x183+162x535+98x718+126x97+3380(mod7). Вариант №15.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №16.
304x622+359x433+191x81+264x231+1380(mod7). Вариант №17.
1082x1983+632x411+197x292+1410(mod11). Вариант №18.
368x663+1354x732+104x671+3430(mod11). Вариант №19.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №20.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №21.
63x708+35x319+426x602+947x394+37x2325+680(mod5). Вариант №22.
213x183+162x535+98x718+126x97+3380(mod7). Вариант №23.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №24.
Многочлены над кольцом классов вычетов

p> 24x3 + 16x — 8 2x+3
6. Вычисление наибольшего общего делителя.
Наибольший общий делитель двух многочленов f и g из кольца R[x] многочленов над полем R может быть найден при помощи алгоритма Евклида. Алгоритм Евклида нахождения наибольшего общего делителя состоит в следующем.
Сначала делят с остатком многочлен f на многочлен g, затем многочлен g — на остаток от первого деления, затем остаток от первого деления — на остаток от второго деления и т.д., пока не получится нулевой остаток.
Это дает следующую цепочку равенств:
rk) и есть наибольший общий делитель многочленовf иg.
Полученный остаток разделим на 9 и выполним третье деление:
Наибольший общий делитель нескольких многочленов f1, f2, …, fm может быть найден индуктивным способом на основании следующей формулы:
Для нахождения линейного выражения наибольшего общего делителя d можно воспользоваться алгоритмом Евклида.
Пример. Найдем линейное выражение наибольшего общего делителя d многочленов f и g из примера 14.
На практике линейное выражение многочлена h удобнее искать не с помощью алгоритма Евклида, а методом неопределенных коэффициентов.
Запишем искомые многочлены u и v в общем виде с неопределенными (неизвестными) коэффициентами.
7. Наименьшее общее кратное.
Теорема Для двух многочленовfиgнаименьшее общее кратное [f, g] связано снаибольшим общим делителем (f, g) соотношением
Из формулы (12) вытекает
Следствие. Наименьшее общее кратное двух взаимно простых многочленов равно их произведению.
8. Сравнения многочленов по многочлену.
Теорема 7. Для любых многочленов и :
Доказательство. Разделим многочлены и с остатком на :
Где — любая из операций (т.е. сравнения можно почленно складывать, вычитать и перемножать).
Доказательство. Из условия, согласно теореме 7, имеем
Складывая, вычитая и перемножая последние равенства, получим:
т.е. обе части сравнения и многочлен можно делить и умножать на один и тот же многочлен.
И теперь эта теорема следует непосредственно из теоремы 7.
Определим на множестве операции сложения и умножения.
Это бы означало, что операции определены некорректно.
Докажем, что определение корректно.
Следовательно, результаты операций над
6.4. Кольцо классов вычетов
Утверждение.— отношение эквивалентности на Z.
Так как — отношение эквивалентности на Z,то Zразбивается на непересекающиесяклассы эквивалентных элементов.
Из утверждениямы получаем, что различных классов помодулю mровно столько, сколько существуетразличных остатков от деления на m,то есть существует mразличных классов, и Zm= <. …,>.
Определим операции сложения и умножения так:
Докажемкорректность нашего определения, тоесть независимость его от выборапредставителей в классах.
Проверим свойства операций.
=+(+)– это свойство ассоциативности сложенияв Zm следует изассоциативности сложения в Z.
элемент по сложению.
Свойства4, 5, 8, 9 из определения кольца следуют изсоответствующих свойств кольца целыхчисел и доказываются так же, как исвойство 1.
Упражнение.Доказать свойства 4, 5, 8, 9.
Такимобразом, мы доказали, что Zm — АКУ-кольцо.
Пример. Выпишем таблицы сложения и умножениядля Z6.
Таккак =,то и в Z6 являются делителями нуля. В то же время=,то есть — обратимый элемент в Z6.








