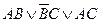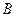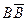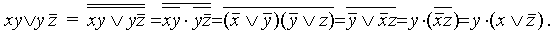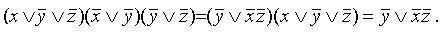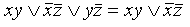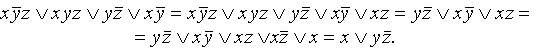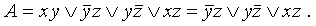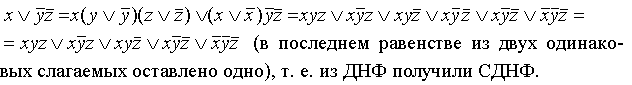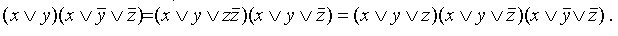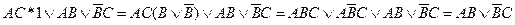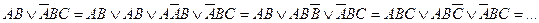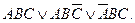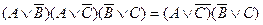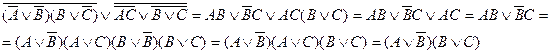дизъюнктивной нормальной формой называется

Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения

Что такое СДНФ

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».

ДНФ выглядит следующим образом:

СДНФ обладает некоторыми определенными свойствами:

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.

Что такое СКНФ

СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

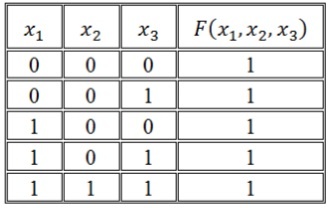
Рассмотрим логическую функцию в виде таблицы истинности.

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

Построим совершенную ДНФ:

И как результат получим следующую СДНФ:

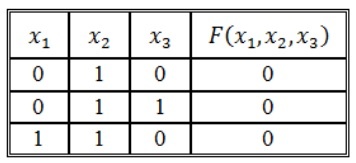
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

Построим совершенную КНФ:

И как результат получим следующую СКНФ:

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Доказать эквивалентность формул можно двумя способами.

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.

Поглощение

Склеивание

Обобщенное склеивание

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)

Расщепление

\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)

Примеры с решением

Задача №1

Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:

\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)

\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)

\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)

\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)

\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)

\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)

Далее приведем выражение к КНФ:

\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)

Далее приведем выражение к СКНФ:

\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)

\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overlinex_2\;\cdot\;\overline\;)\;\vee\;(\overline<\overlinex_2>\;\cdot\;x_3))\;\cdot\;(\overline\;\vee\;x_2)\;=\)

\(=(\overlinex_2\overline\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2)\;\vee\;\overlinex_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2))\;=\)

Источник

Дизъюнктивная нормальная форма

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. [1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Содержание

Примеры и контрпримеры

Построение ДНФ

Алгоритм построения ДНФ

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ

Приведем к ДНФ формулу :

Выразим логические операции → и ↓ через :

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Используя закон дистрибутивности, приводим формулу к ДНФ:

k-дизъюнктивная нормальная форма

k-дизъюнктивная нормальной формой называют дизъюнктивную нормальную форму, в которой каждая конъюнкция содержит ровно k литералов.

Например, следующая формула записана в 2-ДНФ:

Переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостает переменной, например, Z, вставляем в нее выражение :, после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как по закону Идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Формальная грамматика, описывающая ДНФ

Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:

где обозначает произвольную булеву переменную.

См. также

Примечания

Литература

Ссылки

Полезное

Смотреть что такое «Дизъюнктивная нормальная форма» в других словарях:

дизъюнктивная нормальная форма — ДНФ — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации Синонимы ДНФ EN disjunctive normal formDNF … Справочник технического переводчика

дизъюнктивная нормальная форма — norminė disjunkcinė forma statusas T sritis automatika atitikmenys: angl. disjunctive normal form; DNF vok. disjungtive Normalform, f rus. дизъюнктивная нормальная форма, f pranc. forme disjonctive normale, f … Automatikos terminų žodynas

ТУПИКОВАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА — представляющая заданную булеву функцию дизъюнктивная нормальная форма (д. н. ф.), к рую нельзя упростить ни вычеркиванием буквы из нек рой конъюнкции, ни удалением какой либо конъюнкции. Минимальная д. н. ф. получается из сокращенной д. н. ф.… … Математическая энциклопедия

Нормальная форма (математика) — У этого термина существуют и другие значения, см. Нормальная форма (значения). Нормальная форма в математике простейший либо канонический вид, к которому объект приводится эквивалентными преобразованиями[1]. Содержание 1 Жорданова… … Википедия

Нормальная форма (значения) — Нормальная форма: Нормальная форма в базах данных свойство отношения в реляционной модели данных. Нормальная форма в математике в каком либо смысле простейший либо канонический вид, к которому объект приводится преобразованиями,… … Википедия

Конъюнктивная нормальная форма — (КНФ) в булевой логике нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к… … Википедия

СОКРАЩЕННАЯ НОРМАЛЬНАЯ ФОРМА — булевой функции дизъюнктивная нормальная форма (д. н. ф.), представляющая собой дизъюнкцию всех простых импликант данной функции. Конъюнкция наз. импликантой булевой функции f, если справедливо соотношение Импликанта наз. простой, если после… … Математическая энциклопедия

СОВЕРШЕННАЯ НОРМАЛЬНАЯ ФОРМА — совершенная дизъюнктивная или совершенная конъюнктивная нормальная форма (см. Булевых функций нормальные формы) … Математическая энциклопедия

Источник

Дизъюнктивная нормальная форма

Оглавление

определение

Объяснение

Пример: A OR B OR C OR D; A∨B∨C∨D

Отдельные элементы ссылки ИЛИ (A, B, C, D) могут быть более сложными выражениями, которые могут также содержать одну или несколько ссылок И ( соединение ).

как формальное обозначение:

По договоренности скобки и символы (операторы) для ссылки И не записываются.

Оператор НЕ может также присутствовать в таких выражениях:

А. ¯ Б. ¯ С. ¯ ∨ А. ¯ Б. С. ¯ ∨ А. Б. С. ¯ ∨ А. ¯ Б. ¯ С. ∨ А. ¯ Б. С. ∨ А. Б. С. <\ displaystyle <\ bar > <\ bar > <\ bar > \ vee <\ bar > B <\ bar > \ vee AB <\ bar > \ vee <\ bar > <\ bar > C \ vee <\ bar > BC \ vee ABC>

В дополнение к вышеупомянутому требованию о том, что логическое выражение на верхнем уровне состоит исключительно из связей ИЛИ (уровень ИЛИ), на нижних уровнях в квадратных скобках не должно быть дополнительных ссылок ИЛИ. Разрешены только два уровня: верхний уровень ссылок ИЛИ (уровень ИЛИ) и нижний уровень ссылок И (уровень И). Нет более глубокого вложения. Только отрицание может использоваться для элементов уровня И.

образование

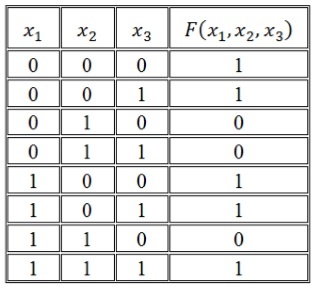
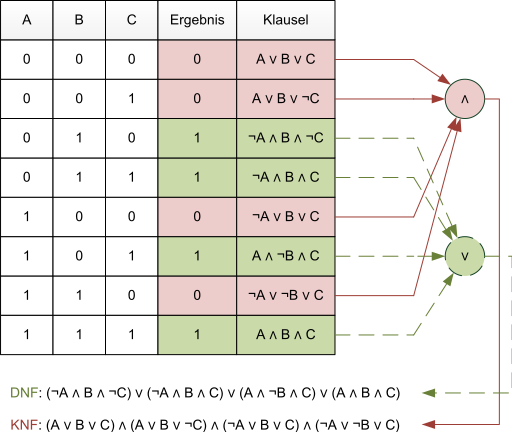
Пример формирования ДНФ

Таблица истинности для этой функции имеет следующий вид:

Функция, представленная в DNF

y знак равно Икс 2 ¯ Икс 1 Икс 0 ¯ ∨ Икс 2 ¯ Икс 1 Икс 0 ∨ Икс 2 Икс 1 ¯ Икс 0 ∨ Икс 2 Икс 1 Икс 0 <\ displaystyle y = <\ bar >> x_ <1><\ bar >> \ vee <\ bar >> x_ <1>x_ <0>\ vee x_ ​​ <2><\ bar >> x_ <0>\ vee x_ ​​ <2>x_ <1>x_ <0>>

также может быть представлено как логическое выражение в квадратных скобках:

е знак равно ( ( Икс 2 ¯ ) ∧ Икс 1 ) ∨ ( Икс 2 ∧ Икс 0 ) <\ Displaystyle е = ((<\ бар >>) \ клин x_ <1>) \ vee (x_ <2>\ клин x_ <0>)>

е знак равно Икс 2 ¯ Икс 1 + Икс 2 Икс 0 <\ displaystyle e = <\ bar >> x_ <1>+ x_ <2>x_ <0>>

Как и в математике, истинность термина продукта определяется путем умножения значений логических переменных. Если одна из задействованных переменных равна нулю, значение всего термина продукта равно нулю; член продукта принимает значение один тогда и только тогда, когда все переменные в нем имеют значение один.

CPLD используют термины продукта, связанные дизъюнктивно (ИЛИ), для определения своей функции.

Каноническая дизъюнктивная нормальная форма

В KDNF те назначения переменных, для которых функция принимает значение 1, выражаются minter terms.

Ортогональная дизъюнктивная нормальная форма

Более нормальные формы

Дизъюнктивная минимальная форма

Источник

«Учебник по дискретной математике ДНФ, СДНФ, КНФ, СКНФ»

Например, 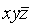является простой конъюнкцией,

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.

Например, выражение 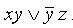является ДНФ.

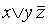
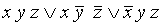
Например, выражение является ДНФ, но не СДНФ. Выражение является СДНФ.

Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.

Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение 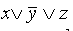– простая дизъюнкция,

Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение 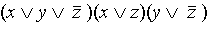– КНФ).

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.

Например, выражение 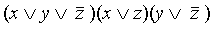является СКНФ.

Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:

а) переход от ДНФ к КНФ

Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:

Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;

б) переход от КНФ к ДНФ

Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)

Таким образом, получили ДНФ.

Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;

в) сокращение ДНФ (или СДНФ) по правилу Блейка

Применение этого правила состоит из двух частей:

— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 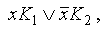, то ко всей дизъюнкции добавляем слагаемое К₁К₂. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;

— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,

Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ 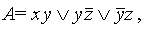, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):

в) переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение 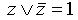,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:

г) переход от КНФ к СКНФ

Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 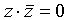(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):

Таким образом, из КНФ получена СКНФ.

Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.

Источник

Дизъюнктивные и конъюнктивные нормальные формы. Совершенные конъюнктивные и дизъюнктивные нормальные формы

Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний. Например: .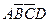

Дизъюнктивно-нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Например: .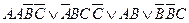

Если учесть, что нулевые конъюнкции можно опустить, а А*А=А, то приведенная ДНФ сведется к более простому виду: .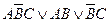

Дальнейшее упрощение получается с помощью законов поглощения: 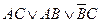. Но полученная формула еще не является минимальной. Можно применить правило, основанное на соображениях симметрии: в рассматриваемой формуле каждая из переменных А, В, встречается два раза, но переменная В встречается один раз с отрицанием, а один раз без отрицания. Значит, симметрия нарушена по переменной В. Тогда тот член дизъюнкции, который эту переменную В не содержит, пропадет, т. е. поглотится АС.

Покажем, что это действительно так:

=

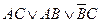
(по закону поглощения ) .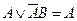

Мы доказали следующее правило поглощения:

Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена только по одной из переменных, то пропадает тот член дизъюнкции, который эту переменную не содержит.

1. . Этот трехчлен содержит два раза , два раза , но один раз и один раз . Значит,, симметрия нарушена по .

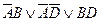
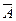
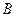
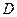
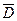
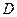
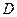
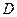
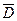
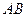
Поэтому, согласно нашему правилу, пропадает член, не содержащий букву (т. е. не содержащий ни , ни ). Значит, надо вычеркнуть .

2. . Этот трехчлен содержит два раза , два раза , но один раз и один раз . Симметрия нарушена по . Значит, вычеркиваем член, не содержащий , т. е. вычеркиваем .

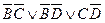
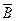
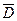
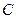
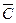
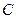
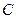
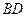
Минимальной мы назовемту ДНФ, которая имеет самую ко­роткую запись.

Существует еще одно правило поглощения, которое тоже основано на соображениях симметрии:

Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена по двум из этих переменных, то данная ДНФ равносильна дизъюнкции, одним из членов которой является пере­менная, по которой симметрия не нарушена, а вторым членом служит тот член первоначальной ДНФ, который эту переменную не содержит.

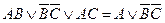
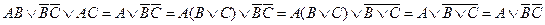
Например: . Покажем, что это действительно так:

.

1. . Этот трехчлен содержит два раза , но содержит по одному разу и , и по одному разу и . Значит, симметрия нарушена дважды: по и по . Симметрия не нарушена только по . Поэтому, применяя наше правило, получим дизъюнкцию, одним членов которой будет , адругим — тот член трехчлена, | который_ не содержит . Значит, получим .

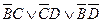
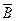
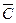
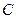
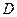
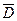
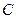
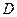
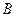
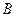
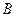
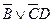
2. .

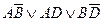
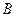
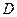
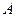
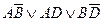
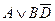
В этом трехчлене симметрия нарушена по и по . Симметрия не нарушена только по . Значит, = .

Для каждой формулы существует бесконечно много различных, но равносильных ей ДНФ. Если, например, найдена одна ДНФ, то путем повторения имеющихся элементарных конъюнкций, добавления нулевых конъюнкций, добавления поглощаемых конъюнкций можно построить бесконечно много новых, но равносильных ей ДНФ.

Например:

Среди всех этих ДНФ есть одна, которая отличаете однородностью и «совершенством» своей формы. Mы имеем в виду формулу:

Она так и называется: «совершенная дизъюнктивно-нормальная форма»(СДНФ).

Дадим точное определение:

СДНФ — это такая ДНФ, которая удовлетворяет следующим условиям:

1. Все элементарные конъюнкции различны.

2. Нет нулевых конъюнкций.

3. Ни одна из элементарных конъюнкций не содержит одинаковых членов.

4. Каждая элементарная конъюнкция содержит все переменные.

Чтобы получить СДНФ, надо сначала найти минимальную ДНФ. Тогда будут выполнены условия 1, 2, 3. Посли этого надо преобразовать эту минимальную ДНФ таким образом, чтобы было выполнено условие 4. Это делается следующим образом:

Приведение формул алгебры высказываний к КНФ виду

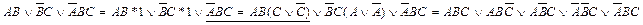
Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например: .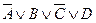

Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например: .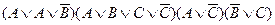

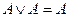
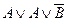
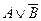
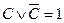
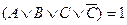
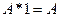
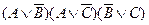
Если воспользоваться равносильностью , то можно заменить через . Кроме того, известно, что, . А если один член дизъюнкции равен 1, то и вся дизъюнкция равна 1. Значит: . Но . Значит, единичный член конъюнкции мож­но просто опустить. Таким образом, первоначальная КНФ| сводится к более простой форме: .

Но эта формула не является еще минимальной. Для КНФ тоже существуют правила поглощения, основанные на соображениях симметрии. Эти правила можно полу­чить по закону двойственности из аналогичных правил, установленных для ДНФ.

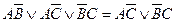
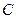
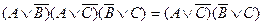
Мы знаем, например, что: (симметрия нарушена по переменной . Поглотилось вы­ражение, не содержащее эту переменную). Запишем теперь двойственную равносильность: . В левой части стоит ранее полученная КНФ. Значит, эту КНФ действительно можно свести к более простой форме.

В то же время мы установили новое правило погло­щения:

Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена только по одной из пере­менных, то поглощается та элементарная дизъюнкция, которая эту переменную не содержит.

Аналогичным образом можно получить и второе пра­вило поглощения, основанное на соображениях симмет­рии. Мы уже знаем, что: .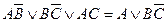

Запишем двойственную равносильность:

Сформулируем соответствующее правило поглощения:

Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по двум из этих пере­менных, то данная КНФ равносильна конъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом является тот член первоначальной КНФ, который эту переменную не содержит.

Чтобы найти минимальную КНФ, равносильную данной формуле, надо эту формулу сначала привести к виду ДНФ, затем надо разложить ее на «множители» и применить законы погло­щения.

Рассмотрим конкретный пример:

Можно поступить и по-другому. Новый подход начнет­ся с того момента, когда была получена формула . В этой формуле симметрия нарушена только по одной переменной . Мы применяли соответ­ствующий закон поглощения. А сейчас мы этого делать не будем. Вместо этого мы добавим к нашей формуле нулевую конъюнкцию, составленную из той переменной, по которой была нарушена симметрия, т. е. добавим и произведем группировку:

Источник