Что такое число ноль
0 (число)
0 (ноль, нуль от лат. nullus — никакой) — целое число, разделяющее на числовой прямой положительные и отрицательные числа. Существуют два подхода к определению натуральных чисел — одни авторы причисляют нуль к натуральным числам, другие этого не делают. В российских школьных программах по математике не принято причислять нуль к натуральным числам, хотя это затрудняет некоторые формулировки (например, приходится различать деление с остатком и деление нацело).
Содержание
Основные свойства нуля
Применение
В математике
В физике
В других областях
Обобщения
Аналог нуля может существовать в любом множестве, на котором определена операция сложения; в высшей алгебре такой элемент называется нейтральным. Чаще всего используется вещественный нуль, то есть нуль в контексте множества вещественных чисел. Другие распространённые вариации:
История
Вавилонские математики использовали особый клинописный значок для шестидесятеричного нуля примерно начиная с 300 г. до н. э., а их учителя-шумеры, вероятно, сделали это ещё раньше.
Своеобразные коды нуля использовали ещё до нашей эры древние майя и их соседи в Центральной Америке (древние майя обозначали ноль стилизованным изображением ракушки).
В Древней Греции число 0 известно не было. В астрономических таблицах Клавдия Птолемея пустые клетки обозначались символом ο (буква омикрон, от др.-греч. ονδεν — ничего); не исключено, что это обозначение повлияло на появление нуля, однако большинство историков признаёт, что десятичный нуль изобрели индийские математики. Без нуля была бы невозможна открытая в Индии десятичная позиционная запись чисел. Первый код нуля обнаружен в индийской записи от 876 г., он имеет вид привычного нам кружочка.
В Европе долгое время нуль считался условным символом и не признавался числом; даже в XVII веке Валлис писал: «Нуль не есть число». В арифметических трудах отрицательное число истолковывалось как долг, а ноль — как ситуация полного разорения. Полному уравнению его в правах с другими числами особенно способствовали труды Леонарда Эйлера.
См. также
Ссылки
Полезное
Смотреть что такое «0 (число)» в других словарях:
число — Прие моч ное Источник: ГОСТ 111 90: Стекло листовое. Технические условия оригинал документа Смотри также родственные термины: 109. Число бетатронных колебаний … Словарь-справочник терминов нормативно-технической документации
Число зверя — … Википедия
Число Зверя — особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с перевёрнутым… … Википедия
Число дьявола — Число зверя особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с… … Википедия
число циклов — Полное количество отдельных выпусков (выбросов) ОТВ для данного устройства импульсного действия. Источник … Словарь-справочник терминов нормативно-технической документации
Число с плавающей запятой — Число с плавающей запятой форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную.… … Википедия
число — сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева
Число Грэма — (Грехема, англ. Graham s number) большое число, которое является верхней границей для решения определённой проблемы в теории Рамсея. Названо в честь Рональда Грэма (англ.). Оно стало известно широкой публике после того, как Мартин … Википедия
ЧИСЛО — ЧИСЛО, числа, мн. числа, чисел, числам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.).… … Толковый словарь Ушакова
Число 23 (фильм) — Роковое число 23 The Number 23 Жанр триллер/драма/детектив … Википедия
Число Ричардсона — ( ) критерий подобия в гидродинамике, равный отношению потенциальной энергии тела, погружённого в жидкость к его кинетической энергии. Под «телом» здесь обычно понимается рассматриваемая жидкость или газ. В общем случае число Ричардсона… … Википедия
Математика с нуля: чем интересно число 0?
Попробуем делить на ноль и узнаем больше об истории и свойствах числа, расположенного ровно посередине числовой оси.
Ноль — это, пожалуй, первое в нашей жизни загадочное число. Мы много слышали, например, о чудесах числа Пи, но мало кто имеет с ним дело в повседневной жизни. Не говоря уже о комплексных числах. А вот с нолём мы сталкиваемся повсюду: даже на клавиатуре обозначающая его цифра завершает ряд.
Но любой понимает, что с этим числом не всё в порядке. В детстве, когда мы ещё думали, что арифметика нужна только для счёта, нам объясняли, что ноль — это отсутствие. И это было странно.
Читайте также :
Поэтому и в истории человечества это число появилось поздно. Торговцы активно использовали счёт, но продавать, например, «ноль овец» не имело смысла. Впрочем, как и отрицательное их количество.
Вышло любопытно: например, древние греки не использовали ноль в принципе, зато уже знали об иррациональных числах, таких как √2. Это было связано с их любовью к геометрии: если у прямоугольного треугольника стороны будут равны 1, длина гипотенузы вычисляется как √2.
Но как же десятеричная система счёта? Ведь даже чтобы записать «10», нам нужен ноль. Но здесь дело только в записи числа: если вы вспомните римские цифры, то поймёте, что десятку можно представить и как Х. Конечно, такая форма была не особенно удобной, но даже вавилоняне, пользовавшиеся позиционной системой счисления (то есть, близкой нашей, а не древнеримской), долго обходились без ноля. Некоторое время его просто не было: числа, скажем, 36 и 306 не различались по написанию и определялись по контексту. Потом его роль стали выполнять два клинышка, вроде вот этих: 3’’6. Но и тогда они самостоятельной роли не играли — не было числа «ноль».
Сложно сказать, когда оно в действительности появилось. При этом есть свидетельства, что в Индии его использовали еще до нашей эры, после чего его переняли арабы — а вот на Западе оно стало входить в практику только в XIII веке усилиями итальянского математика Леонарда Фибоначчи. И то, его любовь к арабскому счислению долго не воспринималась всерьёз.
Известно, что первые слова, обозначавшие количество, имели конкретное применение — «пять лошадей» и «пять лодок» были для древнего человека разными категориями. Чтобы изобрести ноль, требовалось перейти на новый уровень абстрактного мышления.
Но если мы поверим в ноль, его свойства поразят воображение.
Возвести в нулевую степень
Ещё по этой теме :
С самыми простыми операциями проблем не возникает: прибавить ноль или вычесть его из числа — число остаётся тем же, умножить на ноль — получится ноль… Всё это укладывается в рамки здравого смысла. Сложнее становится при возведении в нулевую степень. В школе сообщают, что результатом в каждом случае будет единица. Откуда она взялась?
Тут рассудок уже пасует. Степень — это, как известно, то, сколько раз мы берём число как множитель самого себя.
Если степень нулевая, число не является множителем ни разу, но… как из этой пустоты «родилась» единица?
Чаще всего в школе этот вопрос решается догматически: на объяснения не остаётся желания и сил. А ведь именно здесь пролегает одна из границ, за которой простая арифметика, наглядно показываемая на яблоках и прочих исчислимых вещах, становится уже чистой и прекрасной абстракцией.
Вспомним правила обращения с числами, возводимыми в степень, и представим себе следующий пример:
В отношениях с одинаковыми основаниями степеней мы можем делать следующее:
Так вот чудесным образом, благодаря только принятию ноля как числа, мы переходим к новому странному открытию, и математика совершает куда более далёкий прыжок от реальности, чем просто представление «у меня ноль конфет».
Но именно внутренняя логика системы, которая может быть понята умом, но не может быть представлена в вещественном мире — это и есть красота абстракции.
Поделить на ноль
Это может быть интересно :
«Деление на ноль» давно стало интернет-мемом, правда, довольно неопределённым. То оно означает аннигиляцию чего бы то ни было (а ведь логичнее было бы умножить на ноль), то вовсе разрушение математических основ мироздания. И второе ближе к истине.
Большинство учёных всё-таки считают эту операцию с нолём невозможной или обладающей неопределённым результатом.
В чём же дело, и почему даже машины не могут между собой «договориться»?
Чисто арифметически делимость на ноль приводит к рискованным выводам. Смотрите сами:
Это лишь известное нам свойство ноля. Но если на него можно делить, то, сократив обе части, мы получим:
Почему же речь иногда заходит о бесконечности? Дело в том, что проблему пытаются решить через деление на бесконечно малую функцию, то есть построение графика функции, где x стремился бы к нулю. Так мы пытаемся найти y = 1 / x, и получается следующее:
Кстати говоря, с делением ноля на ноль наблюдается ещё большее единодушие: тут, если мы соберёмся построить функцию, результаты могут быть практически какими угодно (0, ±1, ±∞…) В общем, ноль, оставаясь числом, снова подрывает основы математики, если мы нарушаем неприкосновенность его свойств.
Ноль — чётное число?
Это может быть интересно :
Если он так необычен (и не забываем, что он не является ни положительным, ни отрицательным), можно ли говорить о его чётности? Интуитивно мы догадываемся, что он чётный, ведь целые числа сменяют друг друга именно по такому принципу: 2 — чётное, 1 — нечётное, следующим должно быть снова чётное. Но странность ноля настораживает, подсказывает, что и в этом вопросе нужно держать ухо востро.
Какое главное требование он должен пройти в этом случае? Деление на двойку без остатка, и он выдерживает испытание с достоинством: 0/2=0. Получается целое число 0, причём сколько бы мы ни продолжали деление, результат будет получаться одинаковым — можно сказать, что он является «наиболее» чётным или «бесконечно» чётным числом.
Если быть более точным, мы должны взять другое определение с обратной операцией. Чётное число может быть представлено в виде 2x, где x — целое число, но и в таком случае всё просто: 0 = 2 ∙ 0.
Есть и такое свойство чётных чисел, что при сложении двух из них должно получаться снова чётное, проверим:
При всей необычности ноля даже его удивительное соответствие всем критериям кажется странным, не так ли?
Что смотреть и читать о ноле?
Чтобы узнать больше о ноле как одном из самых загадочных явлений математики, а также об истории его «открытия», вы можете обратиться к следующим ресурсам:
1. Numberphile. Это популярнейший в среде любителей математики Youtube-канал, у которого уже более чем 1,5 миллиона подписчиков. Есть видео и о ноле, которые в переводе на русский можно найти здесь.
2. Книга Чарльза Сейфе «Ноль. Биография опасной идеи». Автор, хоть и не без излишнего сгущения красок, рассказывает об истории ноля как числа и цифры — причем в обширном контексте истории науки, от Архимеда до теории струн. В качестве бонуса вы получите приложения с задачками, где используется ноль. Например, вам предложат доказать, что Уинстон Черчилль был морковкой, и построить машину времени из кротовой норы.
3. Сборник эссе, в которых фантаст Айзек Азимов рассказывает о том, как человек, переходя от счёта на пальцах ко всё более сложным вычислениям, разработал основные математические операции, а также о том, как числа связаны с нашим восприятием времени и пространства. Природе ноля и его парадоксам посвящена открывающая книгу статья «Nothing Counts».
Даже если вам не нравились в школе ни арифметика, ни алгебра, у вас всегда есть возможность ими заинтересоваться. Учить математику с нуля уже не получится — худо-бедно мы начали считать ещё дошколятами. А вот полюбить её с нуля — вполне реальная перспектива.
Ноль (цифра)
Ноль (нуль, от лат. nullus — никакой) — название первой (по порядку) цифры в стандартных системах исчисления, а также математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех левее стоящих цифр на разряд (например, в десятичной системе счисления, умножает на десять). Сравните, например, числа 410 и 4010; 416 и 4016 (нижний индекс означает основание системы счисления).
Содержание
История
В Индии
Индийцы называли знак, обозначающий отсутствие какого-либо разряда в числе, словом «сунья», что значит пустой (разряд, место, см. Шуньята). Арабы перевели это слово по смыслу и получили слово «сифр».
Первое достоверное свидетельство о записи нуля относится к 876 г.; в настенной надписи из Гвалиора (Индия) имеется число 270. Некоторые исследователи предполагают, что нуль быль заимствован у греков, которые ввели в качестве нуля букву «о» в шестидесятеричную систему счисления, употребляемую ими в астрономии.
Другие, наоборот, считают, что ноль пришёл в Индию с востока, он был изобретён на границе индийской и китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого кружка.
Индийцы вначале обозначали нуль точкой.
В Европе
Леонардо Пизанский (1228) употребил для передачи арабского термина «сифр» слово zephirum (латинское слово zephyrus — зефир означало западный ветер), а одновременно с ним другой главный поборник индийской нумерации в Европе, Иордан Неморарий (1237), употребляет арабскую форму cifra.
С начала XVI века в немецких руководствах слово «цифра» получает значение современное, слово «нуль» входит в повсеместное употребление в Германии и в других странах, сначала как слово чужое и в латинской грамматической форме, постепенно принимая форму, свойственную данному национальному языку.
В России
Ноль в других культурах
Майя использовали ноль в своей двадцатеричной системе счисления почти на тысячелетие раньше индийцев. Первая сохранившаяся стела с датой календаря майя датируется 7.16.3.2.13, 6 Бен 16 Шуль 10 декабря 36 года до н. э..
В империи инков Тауантинсуйу для записи числовой информации использовалась узелковая система кипу, основанная на позиционной десятеричной системе счисления. Цифры от 1 до 9 обозначались узелками определённого вида, ноль — пропуском узелка в нужной позиции. В современном кечуа ноль обозначается словом кечуа ch’usaq (букв. «отсутствующий», «пустой»), однако то, какое слово использовалось инками для обозначения нуля при чтении кипу, пока неясно, поскольку, например, в одних из первых кечуа-испанских (Диего Гонсалес Ольгин, 1608) словарях и первом аймара-испанском (Лудовико Бертонио, 1612) не было соответствия для испанского «cero» — «ноль».
Что такое число ноль
Однажды на уроке математики при решении примеров я задумалась, что это за число «0», откуда оно взялось, и кто мог его придумать?
Я знала, что ноль — это нейтральный элемент для операций сложения и вычитания. Умножение любого элемента множества на ноль дает ноль. Ноль не изменяет значения числа при прибавлении к нему или вычитании из него.
Актуальность исследования: в математике число нуль обладает удивительной силой. Без нуля не было бы всей математики. Без нуля не существовала бы современная компьютерная техника. А представить себе современную жизнь без компьютера также трудно, как и то, что когда-то наши предки испытывали ужас перед цифрой нуль.
Объектом исследования данной работы является цифра и число ноль.
Цель работы: расширить знания о числе нуль, приоткрыть завесу тайн, связанных с этим числом.
под о брать литературу для исследования;
изучить учебную, энциклопедическую, занимательную литературу;
ознакомиться с понятием «ноль», историей возникновения нуля;
провести социологический опрос;
собрать и решить задачи по данной теме.
Методы решения: поиск, изучение, анализ, обобщение, классификация.
Практическая значимость: собранная и изученная информация о нуле расширит мои знания о математике.
1.1 История возникновения цифры «НОЛЬ»
1.2 Интересные факты о цифре «0»
1. Число «0» в обычных арифметических операциях ведет себя совершенно уникально:
2. Число «0» — это единственное число, на которое нельзя делить.
3. Число «0» — это единственное действительное число, которое не является ни положительным, ни отрицательным.
4. В центре города Будапешт (Венгрия) находится памятник НУЛЮ.
Цифра означает начало всех дорог по Венгрии. От этого памятника отмеряются все расстояния в стране.
Нуль — это единственная цифра, которой поставлен памятник.
5. Число 0 имеет два названия: НУЛЬ и НОЛЬ.
Оба названия в свободном употреблении — равноправны. Но в некоторых устойчивых выражениях эти слова не взаимозаменяемы. Например, только нуль в выражениях: остричь под нуль; быть равным нулю; начать с нуля; свести к нулю.
Но только ноль в таких выражениях: ноль-ноль; ноль внимания; ноль без палочки.
6. Абсолютный НУЛЬ температуры — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы. По шкале Цельсия абсолютному нулю соответствует температура −273,15° C.
8. Первая цифра натурального числа может быть любой, кроме цифры «О».
9. В полночь на электронных часах появляются четыре НУЛЯ.
Начинается новый день!
10. КРЕСТИКИ-НОЛИКИ — логическая игра, в которой один из игроков играет “крестиками”, а второй — “ноликами”.
11. Только цифра «0» пишется точно так же, как одна из букв — а именно, как буква О[2].
Раньше цифра писалась с черточкой внутри знака (иногда, как пишется греческая буква Тэта), чтобы отличать ее от буквы О.
Ноль без этой палочки был то ли цифрой, то ли буквой. Поэтому и стали иногда говорить “НОЛЬ БЕЗ ПАЛОЧКИ”,
Бронзовый знак символически обозначает начало всех российских дорог, точку отсчёта их расстояний; он выполнен в виде компаса, вмонтированного в брусчатку площади. В центре размещён небольшой круглый пятачок с розой ветров (уже практически стёршейся), числом «0» и подписью «Нулевой километр автодорог Российской Федерации», а вокруг него, образуя по периметру ровный квадрат – 4 угла-стрелки, указывающие на север, юг, запад и восток. На углах выгравированы изображения животных, характерных для фауны расположенных в соответствующей стороне света регионов: олень, полярная сова, тюлень на севере, дельфин, тур и гриф на юге, зубр, глухарь и угорь на западе, тигр, тукан и кобра на востоке.
Квадратный знак вписан в бронзовую окружность, которая в свою очередь заключена в квадрат из крупной чёрной плитки.
14. Замкнутая орбита любого космического тела — это ЭЛЛИПС, который по форме полностью совпадает с формой цифры «0».
15. На клавиатуре компьютера цифры изображают в таком порядке
Эта числовая последовательность является ПОЧТИ возрастающей. Нарушает порядок только лишь цифра «О» [11].
2. Практическая часть
2. 1. Математические действия с цифрой «0»
Ноль — это нейтральный элемент для операции сложения (то есть при сложении с нулём число не меняется). Умножение любого элемента множества на ноль даёт ноль.
2.2. Доказательство. Почему нельзя делить на ноль?
Деление, это операция, обратная умножению. То есть, деление числа А на число Б – это поиск такого числа С, которое при умножении на число Б дает в результате число А. То есть: если А:Б=С то Б•С=А.
А почему 0 на 0 нельзя? Ведь 0•0 равно 0. Значит, если 0 разделить на 0, должен получиться 0! Правильно? Правильно, да не совсем. 1•0 то же будет ноль. И 5•0 то же будет ноль. Так почему при делении ноль на ноль должен именно ноль получиться? Ведь так рассуждая, в результате может быть любое число. А математики говорят, что получится «неопределенность». А в школьном курсе, просто считается: «На ноль делить нельзя!»[7].
Опрос по теме: «НОЛЬ – УДИВИТЕЛЬНЫЙ И НЕВЕРОЯТНЫЙ»
Для того, чтобы узнать насколько мои родственники, друзья и одноклассники осведомлены о происхождении и свойствах цифры «0» я провела анкету (см. Приложение 1 Анкета). Всего отвечали: взрослых возрастом от 24 до 67 лет– 8 чел., детей – от 7 до 12 лет – 18 чел.
1. Как правильно говорить «ноль» или «нуль»?
Неправильно – 22 чел
2. Знаете ли Вы, как появилось выражение «ноль без палочки»?
Да – 15 чел, нет – 11 чел
Опрос показал, что большинство моих современников:
— не знают о том, что правильно говорить и «ноль» и «нуль»;
— не осведомлены о том, как появилось выражение «ноль без палочки»;
Итак, опрос показал, что о свойствах цифры «0» большинство опрошенных не знают. Больше всего меня удивило что многие взрослые и мои ровесники при ответе на последний вопрос забыли правило, что на ноль делить нельзя![3]
2.3 Задачи по теме «Ноль – удивительный и невероятный»
1. На доске написано 15 чисел: 8 нулей и 7 единиц. Вам предлагается 14 раз подряд выполнить такую операцию: зачеркиваем любые два числа, и если они одинаковые, то дописываем к оставшимся числам нуль, а если равные, то единицу. Какое число останется на доске?
2. Чему равна сумма чисел от 1 до 100?
3. Сколькими нулями заканчивается произведение всех натуральных чисел от1 до 100?
4. Расставить в клетках числа от 1 до 8 так, чтобы в любом направлении получилось в сумме 12. (Число 0 стоит во второй строке, в третьей клетке).
6. Найти все двузначные числа, не содержащие цифры 0 и делящиеся на сумму своих цифр.
7. Только одна из цифр четырёхзначного числа – нуль. Если его зачеркнуть, то число уменьшится в 9 раз. Найдите это число.
8. Сумма двух чисел 715. Одно число заканчивается нулём. Если этот ноль зачеркнуть, то получится второе число. Найди эти числа. Сделай проверку[8].
2.4 Итоги практической части «Решение задач»
Нулевое число (0)
Определение нулевого числа
Когда на столе 2 яблока и мы берем 2 яблока, мы можем сказать, что на столе нет яблок.
Нулевое число не является положительным и отрицательным числом.
Ноль также является цифрой-заполнителем в других числах (например: 40,103, 170).
Нулевая цифра
При написании чисел нулевая цифра используется в качестве заполнителя.
204 = 2 × 100 + 0 × 10 + 4 × 1
История нулевых номеров
Кто придумал нулевое число?
Современный символ 0 был изобретен в Индии в VI веке, позже использовался персами и арабами, а затем и в Европе.
Символ нуля
В арабской системе счисления используется символ ٠.
Свойства с нулевым числом
x представляет любое число.
| Операция | Правило | пример |
|---|---|---|
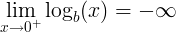 | ||
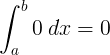 |
Нулевое дополнение
Сложение числа плюс ноль равно числу:
Нулевое вычитание
Вычитание числа минус ноль равно числу:
Умножение на ноль
Умножение числа на ноль равно нулю:
Число деленное на ноль
Деление числа на ноль не определено:
x ÷ 0 не определено
5 ÷ 0 не определено
Ноль делится на число
Деление нуля на число равно нулю:
Число в нулевой степени
Степень числа, возведенного в ноль, равна единице:
Логарифм нуля
Логарифм нуля по основанию b не определен:
Нет числа, с которым мы могли бы поднять основание b до нуля.
Только предел логарифма x по основанию b, когда x сходится к нулю, равен минус бесконечности:
Наборы, содержащие ноль
| Установить | Установить обозначение членства |
|---|---|
| Натуральные числа (неотрицательные) | 0 ∈ ℕ 0 |
| Целые числа | 0 ∈ ℤ |
| Вещественные числа | 0 ∈ ℝ |
| Сложные числа | 0 ∈ ℂ |
| Рациональное число | 0 ∈ ℚ |
Набор четных чисел:
Набор нечетных чисел:
Ноль является членом набора четных чисел:
Есть два определения набора натуральных чисел.
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
У целых чисел есть три определения:
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора целых чисел и набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
Ноль входит в набор целых чисел:
Является ли ноль рациональным числом?
Ноль можно записать как частное двух целых чисел.
Положительное число определяется как число больше нуля:
Поскольку ноль не больше нуля, это не положительное число.
Число 0 не является простым числом.
Ноль не является положительным числом и имеет бесконечное количество делителей.







