Что такое энергия ферми

Энергия Ферми

Вырожденный электронный газ в металле.

Распределение электронов по различным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Принцип Паули вынуждает электроны взбираться вверх «по энергетической лестнице».

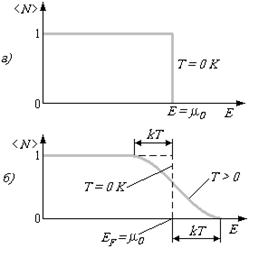
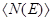
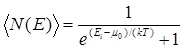
Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми-Дирака. Если μ₀ – химический потенциал электронного газа при T = 0 К, то, среднее число электронов в квантовом состоянии с энергией Е равно

(1)

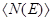
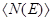
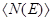
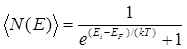
Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов = f(Е), где f(Е) – функция распределения электронов по состояниям. Из (1) следует, что при Т = 0 К функция распределений = 1, если E μ₀,. График этой функции приведен на рис. 15, а. В области энергий от 0 до μ₀ функция равна единице. При E = μ₀ она скачкообразно изменяется до нуля. Это означает, что при Т = 0 К все нижние квантовые состояния, вплоть до состояния с энергией E = μ₀, заполнены электронами, а все состояния с энергией, большей μ₀, свободны. Следовательно, μ₀ есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Фермии обозначается Е_F.( Е_F = μ₀). Поэтому распределение Ферми — Дирака обычно записывается в виде

(2)

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми.Уровню Ферми соответствует энергия Ферми Е_F:, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. с. от верхнего из занятых электронами энергетических уровней.

Для металлов при не слишком высоких температурах выполняется неравенство kT 4 К, т.е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.

Если (Е — Е_F) >> kТ («хвост» функции распределения), то единицей в знаменателе (2) можно пренебречь по сравнению с экспонентой и тогда распределение Ферми — Дирака переходит в распределение Максвелла — Больцмана.

Источник

Энергия Ферми

Энергия Фе́рми () системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Энергия Ферми — одно из центральных понятий физики твёрдого тела.

Физический смысл уровня Ферми: вероятность обнаружения частицы на уровне Ферми составляет 0,5 при любых температурах, кроме T = 0.

Название дано в честь итальянского физика Энрико Ферми.

Фермионы — частицы с полуцелым спином, обычно 1/2, такие как электроны — подчиняются принципу запрета Паули, согласно которому две одинаковые частицы не могут занимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми — Дирака. Основное состояние невзаимодействующих фермионов строится начиная с пустой системы и постепенного добавления частиц по одной, последовательно заполняя состояния в порядке возрастания энергии. Когда необходимое число частиц достигнуто, энергия Ферми равна энергии самого высокого заполненного состояния (или самого низкого незанятого состояния; различие не важно, когда система является макроскопической). Поэтому энергию Ферми называют также уровнем Фе́рми. Частицы с энергией равной энергии Ферми двигаются со скоростью называемой скоростью Фе́рми.

В свободном электронном газе (квантовомеханическая версия идеального газа фермионов) квантовые состояния могут быть помечены согласно их импульсу. Кое-что подобное можно сделать для периодических систем типа электронов, движущихся в атомной решётке металла, используя так называемый квазиимпульс (Частица в периодическом потенциале). В любом случае, состояния с энергией Ферми расположены на поверхности в пространстве импульсов, известной как поверхность Ферми. Для свободного электронного газа, поверхность Ферми — поверхность сферы; для периодических систем, она вообще имеет искаженную форму. Объем заключённый под поверхностью Ферми определяет число электронов в системе, и её топология непосредственно связана с транспортными свойствами металлов, например, электрической проводимостью. Поверхности Ферми большинства металлов хорошо изучены экспериментально и теоретически.

Уровень Ферми при ненулевых температурах

При ненулевой температуре ферми-газ не будет являться вырожденным, и населённость уровней будет плавно уменьшаться от нижних уровней к верхним. В качестве уровня Ферми можно выбрать уровень, заполненный ровно наполовину (то есть вероятность находящегося на искомом уровне состояния быть заполненным частицей должна быть равна 1/2).

Энергия Ферми свободного ферми-газа связана с химическим потенциалом уравнением

где — энергия Ферми, — постоянная Больцмана, и — температура. Следовательно, химический потенциал приблизительно равен энергии Ферми при температурах намного меньше характерной температуры Ферми . Характерная температура имеет порядок 10 5 K для металла, следовательно при комнатной температуре (300 K), энергия Ферми и химический потенциал фактически эквивалентны. Это существенно, потому что химический потенциал не является энергией Ферми, которая входит в распределение Ферми — Дирака.

См. также

Литература

Гусев В. Г., Гусев Ю. М. Электроника. — М.: Высшая школа, 1991. — С. 53. — ISBN 5-06-000681-6.

Источник

Что такое энергия ферми

История развития коллоидной химии

Студентам

Знакомимся ближе

Разделы

Уровень Ферми

Вероятность нахождения электрона на том или ином энергетическом уровне при температуре Т определяется функцией Ферми – Дирака:

где W_F – энергетический уровень, называемый уровнем Ферми.

При Т=0°К вероятность занятия электронами уровней W > W_F равна нулю:

а уровней W W_F, а энергетические уровни ВЗ – условию W 0°К появляется небольшая вероятность занятия электронами уровней в ЗП, а вероятность занятия уровней в ВЗ соответственно снижается.

Из формулы Ферми – Дирака видно, что при температуре, отличной от абсолютного нуля (Т>0), уровень Ферми – это такой энергетический уровень W = W_F, формальная вероятность заполнения которого электроном равна 0,5 (т.к. е° = 1).

Формальное потому, что уровень Ферми находится в запрещенной зоне и фактически не может быть занят электроном. Таким образом, конкретный смысл имеют только те участники кривой распределения f_n(W), которые расположены в ЗП и в ВЗ.

Кривая распределения Ферми – Дирака всегда симметрична относительно уровня Ферми. Из этого, в частности, следует, что в собственном полупроводнике уровень Ферми расположен посередине ЗЗ. При повышении температуры от нуля появляется определенная вероятность занятия электронами энергетических уровней в ЗП. Но при этом на такую же величину снижается вероятность нахождения электронов в ВЗ. Нетрудно видеть, что при симметричном размещении кривой распределения f_n(W) относительно уровня Ферми это возможно только в случае, если уровень Ферми будет находиться посередине ЗЗ.

Источник

Энергия Ферми

Согласно квантовой механике, фермионы — частицы с полуцелым спином, обычно 1/2, такие как электроны — подчиняются принципу запрета Паули, который гласит, что никакие две частицы не могут занимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми-Дирака. Основное состояние невзаимодействующих фермионов строится начиная с пустой системы и постепенного добавления частиц по одной, последовательно заполняя наименьшие энергетические состояния. Когда необходимое число частиц достигнуто, энергия Ферми — энергия самого высокого заполненного состояния (или, эквивалентно, самое низкое незанятое состояние; различие не важно, когда система является макроскопической). Поэтому энергию Ферми называют также уровнем Ферми.

Уровень Ферми при положительных температурах

При положительной температуре ферми-газ не будет являться вырожденным, и населённость уровней будет плавно уменьшаться от нижних уровней к верхним. В качестве уровня Ферми можно выбрать уровень, заполненный ровно наполовину (т.е. вероятность находящегося на искомом уровне состояния быть заполненным частицей должна быть равна 1/2).

Энергия Ферми свободного ферми-газа связана с химическим потенциалом уравнением

где E_F — энергия Ферми, k — постоянная Больцмана, и T — температура. Следовательно, химический потенциал приблизительно равен энергии Ферми при температурах намного меньше характерной температуры Ферми E_F/k. Характерная температура имеет порядок 10 5 K для металла, следовательно при комнатной температуре (300 K), энергия Ферми и химический потенциал фактически эквивалентены. Это существенно, потому что химический потенциал не является энергией Ферми, которая входит в распределение Ферми-Дирака.

Литература

Гусев В.Г., Гусев Ю.М. Электроника. — М.: Высшая школа, 1991. С. 53. ISBN 5-06-000681-6

Источник

Энергия Ферми

Из Википедии — свободной энциклопедии

Энергия (уровень) Фе́рми ( E F <\displaystyle E_> ) системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в её основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Энергия Ферми — одно из центральных понятий физики твёрдого тела.

Название дано в честь итальянского физика Энрико Ферми.

Фермионы — частицы с полуцелым спином, обычно 1/2, такие как электроны — подчиняются принципу запрета Паули, согласно которому две одинаковые частицы, образуя квантово-механическую систему (например, атом), не могут принимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми — Дирака. Основное состояние невзаимодействующих фермионов строится начиная с пустой системы и постепенного добавления частиц по одной, последовательно заполняя состояния в порядке возрастания их энергии (например, заполнение электронами электронных орбиталей атома). Когда необходимое число частиц достигнуто, энергия Ферми равна энергии самого высокого заполненного состояния (или самого низкого незанятого состояния: в случае макроскопической системы различие не важно). Поэтому энергию Ферми называют также уровнем Фе́рми. Частицы с энергией, равной энергии Ферми, двигаются со скоростью, называемой скоростью Фе́рми (только в случае изотропного дисперсионного соотношения в среде).

В свободном электронном газе (квантово-механическая версия идеального газа фермионов) квантовые состояния могут быть помечены согласно их импульсу. Нечто подобное можно сделать для периодических систем типа электронов, движущихся в атомной решётке металла, используя так называемый квазиимпульс (Частица в периодическом потенциале). В любом случае, состояния с энергией Ферми расположены на поверхности в пространстве импульсов, известной как поверхность Ферми. Для свободного электронного газа, поверхность Ферми — поверхность сферы; для периодических систем она вообще имеет искаженную форму. Объём, заключённый под поверхностью Ферми, определяет число электронов в системе, и её топология непосредственно связана с транспортными свойствами металлов, например, электрической проводимостью. Поверхности Ферми большинства металлов хорошо изучены экспериментально и теоретически.

Источник