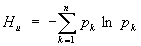Что такое энтропия глаз

Что такое энтропия?

в Заболевания глаз 15.10.2019 0 56 Просмотров

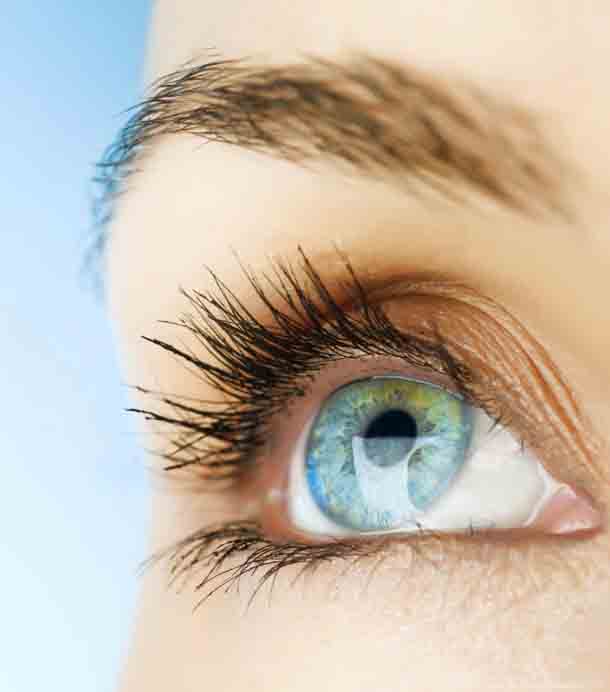
Энтропия – это состояние глаз, при котором край века скатывается в глаз. Обычно это вызывает боль и дискомфорт, потому что ресницы тянутся по деликатной поверхности глаза, когда веко закатывается. Это состояние очень легко поддаётся лечению, и рекомендуется начать лечение рано, чтобы избежать необратимого повреждения глаза. Офтальмолог может очень быстро диагностировать энтропию у пациента и обеспечить временное облегчение, такое как смазывающие капли, которые можно использовать до тех пор, пока пациент не сможет прийти на операцию по восстановлению века.
Иногда энтропия является результатом инфекции или травмы глаза, которая повреждает веко. В других случаях люди рождаются с этим условием. У некоторых пациентов веки постоянно поворачиваются, в то время как у других большую часть времени веки могут находиться в нормальном положении, когда веки поворачиваются, когда они чихают, вытирают глаза или качают головой.

Ключевой проблемой энтропии является раздражение, вызываемое ресницами. Люди могут испытывать зуд, боль и покраснение глаз, и они обычно вызывают много слёз и со временем начинают развиваться проблемы со зрением. Иногда роговица заражается из-за раздражения. У младенцев с энтропией ресницы обычно достаточно мягкие, и могут не вызывать сильного раздражения, но глаза ребенка могут казаться слегка раздраженными или слезящимися.

Лечение энтропии – операция. В ходе операции врач слегка меняет структуру века, чтобы вытащить веко и удержать его на месте. Время заживления обычно довольно быстрое, и облегчение от раздражения является немедленным, так как ресницы больше не тянутся через роговицу с каждым миганием. Врач может назначить антибиотики или противовоспалительные препараты после операции, чтобы вылечить инфекцию или раздражение и помочь прояснить глаза.

Источник

Все меняется, и некоторым из нас это не всегда нравится. Но согласно одной из точек зрения, энтропия Вселенной и природы в целом (то есть степень беспорядка или случайности в системе) может быть тем, что в первую очередь способствовало возникновению жизни.

реклама

Согласно этой точке зрения, когда группа атомов приводится в движение внешним источником энергии, например Солнцем, и окружена источником тепла, например атмосферой, она постепенно перестраивается таким образом, чтобы рассеивать все больше энергии. С этого момента, при определенных условиях, материя неумолимо приобретает свойства, ассоциирующиеся с жизнью.

Однако энтропию также связывают с тепловой смертью Вселенной. Вот все, что необходимо знать об энтропии в термодинамике и о том, как она влияет на Вселенную и, в конечном счете, на нас.

Что такое энтропия Вселенной?

Хотя в физике это не одно и то же, полезно вспомнить о теории хаоса и о том, как она связана с энтропией, и, в конечном счете, какое влияние энтропия может оказывать на Вселенную.

реклама

Согласно теории хаоса, в кажущейся случайности хаотических, сложных систем есть скрытые закономерности и взаимосвязи. Если знать начальные условия и выяснить эти базовые закономерности, то можно предсказать нарушения, которые произойдут в будущем. Другими словами, хаос не так беспорядочен и случаен, как может показаться.

В своей самой простой формулировке энтропия определяется как мера тепловой энергии в системе на единицу температуры, которая не может быть использована для совершения полезной работы. Поскольку работа получается в результате упорядоченного движения молекул, энтропия также является мерой молекулярного беспорядка, или случайности, в системе.

Не только физика, но и многие дисциплины нашли применение этой концепции, включая химию, биологию, изменение климата, социологию, экономику, теорию информации и даже бизнес.

Но давайте остановимся на физике, а точнее, на фундаментальных законах термодинамики.

Кто ввел понятие энтропии?

реклама

Несмотря на то, что понятие энтропии применяется в различных дисциплинах, оно берет свое начало в физике. Изучая сохранение механической энергии в своей работе » Основные принципы равновесия и движения» (1803), французский математик Лазар Карно предложил, что ускорения и удары движущихся частей в машине представляют собой «потери момента активности». Момент активности» Карно сопоставим с современным понятием работы в термодинамике. Таким образом, в любом естественном процессе существует неотъемлемая тенденция к рассеиванию полезной энергии.

Другие ученые исследовали эту «потерянную» энергию, и в последней половине 19 века они указали, что это не настоящее исчезновение, а преобразование. Это и есть концепция сохранения энергии, которая проложила путь к первому закону термодинамики. Такие ученые, как Джеймс Джоуль, Юлиус Майер, Герман Гельмгольц и Уильям Томпсон (также известный как лорд Кельвин), опубликовали работы, исследующие эту концепцию.

реклама

Но термин «энтропия» появился в работах немецкого физика Рудольфа Клаузиуса, который сегодня считается одним из авторов термодинамики.

В 1850-х годах он представил изложение Второго закона термодинамики применительно к тепловому насосу. Заявление Клаузиуса подчеркивало тот факт, что невозможно построить устройство, работающее по циклу и не производящее никакого другого эффекта, кроме передачи тепла от более холодного тела к более горячему.

В 1860-х годах он придумал слово «энтропия» от греческого слова, означающего превращение, или поворотный пункт, для обозначения необратимой потери тепла. Он описал ее как функцию состояния в термодинамическом цикле, в частности в цикле Карно, теоретическом цикле, предложенном сыном Лазаря Карно, Сади Карно.

В 1870-х годах австрийский физик и философ Людвиг Больцман переосмыслил и адаптировал определение энтропии к статистической механике. Ближе к тому, что подразумевает этот термин сейчас, он описывает энтропию как измерение всех возможных микро-состояний в системе, макроскопическое состояние которой было изучено. Как могут измениться все наблюдаемые свойства системы? Сколькими способами? Эти вопросы охватывают понятие беспорядка, которое лежит в основе одного из понятий энтропии.

Находится ли Вселенная в состоянии энтропии?

Еще в 19 веке Рудолф Клаузиус вывел, что энергия Вселенной постоянна, а ее энтропия имеет тенденцию к увеличению с течением времени.

По мнению космологов, затем эта точка «взорвалась», расширяясь и распространяясь со скоростью, превышающей скорость света, и породив все частицы, античастицы и излучения во Вселенной.

Конечно, для этого должно было произойти огромное количество процессов связанных с изменением энтропии. Однако если мы подумаем о непрерывном увеличении энтропии, которое происходило на протяжении всех этих лет, то сможем сделать вывод, что энтропия Вселенной сейчас должна быть намного больше. На самом деле, согласно расчетам, энтропия Вселенной сегодня примерно в квадриллион раз больше, чем во время Большого взрыва.

Почему энтропия Вселенной растет?

Черные дыры обладают огромной концентрацией массы, которая обеспечивает им исключительно сильное гравитационное поле. Поэтому они допускают множественность микросостояний. В связи с этим Стивен Хокинг предположил, что черные дыры выделяют тепловое излучение вблизи своих горизонтов событий. Это излучение Хокинга может привести к потере массы и окончательному испарению черных дыр.

Но помните, что черные дыры подчиняются второму закону термодинамики, который гласит, что энтропия всегда будет иметь тенденцию к увеличению. Поэтому они будут набирать все большую массу и сливаться с другими черными дырами, превращаясь в сверхмассивные чёрные дыры. А когда они в конце концов распадутся, излучение Хокинга, создаваемое распадающимися чёрными дырами, будет иметь такое же количество возможных состояний, как и сама ранее существовавшая черная дыра. Согласно этой точке зрения, ранняя Вселенная имела низкую энтропию из-за меньшего количества или гораздо меньших размеров черных дыр.

Существует ли предел энтропии во Вселенной?

Как бы мы ни говорили о тенденции к увеличению энтропии, законы термодинамики также подразумевают состояние максимальной энтропии.

В повседневной жизни мы можем наблюдать это, когда наш кофе остывает в чашке. Когда кофе достигает комнатной температуры, это означает, что он находится в тепловом равновесии с окружающей средой. В кипящей воде, используемой для приготовления кофе, было много возбужденных атомов, но они замедлились и в конце концов достигли максимальной энтропии для данной системы.

При постоянной, стабильной температуре во всем космосе больше не останется энергии для совершения работы, так как энтропия достигнет максимального уровня. Все эти предположения составляют теорию тепловой смерти Вселенной. Эта теория также известна под названием «Большой заморозки», поскольку в этом сценарии энтропия Вселенной будет постоянно возрастать, пока не достигнет максимального значения. В этот роковой момент все тепло в нашей Вселенной будет распределено абсолютно равномерно, не оставляя места для полезной энергии.

Может ли энтропия Вселенной уменьшиться?

Можно с уверенностью сказать, что энтропия во Вселенной в какой-то момент уменьшилась, потому что в ней существует определенный порядок. Гравитационные взаимодействия могут к примеру превращать туманности в звезды. Это своего рода порядок.

Энтропия может уменьшаться без нарушения второго закона термодинамики до тех пор, пока она увеличивается в других частях системы. В конце концов, второй закон термодинамики не говорит, что энтропия не может уменьшаться в определенных частях системы, а только то, что общая энтропия системы имеет естественную тенденцию к увеличению.

При этом общая энтропия Вселенной не уменьшается. Как было сказано выше, энтропия будет иметь тенденцию к увеличению, пока не достигнет своего максимального уровня и не приведет к тепловой смерти. Это стационарное состояние термодинамического равновесия, в котором энтропия не только максимальна, но и постоянна, и она будет оставаться такой, пока не произойдет приток энергии, который оживит систему.

Тогда цикл может повториться. С новой, дополнительной энергией, совершающей работу, останется часть энергии, не способной совершить работу, которая превратится в тепло. Это снова увеличит энтропию системы. Но откуда возьмется эта энергия? Что заставит оставшиеся лептоны и фотоны, если таковые имеются, взаимодействовать?

Источник

интропия

Задайте вопрос и получите качественную консультацию врачей. Для вашего удобства консультации доступны и в мобильном приложении. Не забывайте благодарить врачей, которые вам помогли! На портале действует акция «Поблагодарить – это просто»!

Вы врач и хотите консультировать на портале? Ознакомьтесь с инструкцией «Как стать консультантом».

Уважаемые консультанты, обратите внимание, что давать назначения или прямые указания по применению препаратов задающим вопросы – запрещено! Пожалуйста, ознакомьтесь с правилами работы консультантов на нашем портале.

Для вас всегда работает специальный раздел для нашего совместного общения и публикации новостей о работе раздела консультаций. Уделите ему внимание и посещайте время от времени. Там будут публиковаться все новости о доработках раздела и его формате работы – где вы можете задать любые интересующие вас вопросы.

Для экстренной связи с администрацией портала используйте нашу почту: mlab@medihost.ru

Спасибо за то, что вы с нами!

—> Мы открыли специальный раздел для нашего совместного общения и публикации новостей о работе раздела консультаций.Уделите ему внимание и посещайте время от времени. Там будут публиковаться все новости о доработках раздела и его формате работы.

—> В ближайшее время мы планируем большое обновление функционала выплаты бонусов для консультантов портала. Информация по этому обновлению так же будет опубликована на форуме в соотвествующем разделе. Ждите новостей!

—> Мы так же призываем использовать этот раздел форума для общения с нами по любым вопросам.

—> Уважаемые консультанты, обратите внимание, что давать назначения или прямые указания по применению препаратов задающим вопросы – запрещено! Пожалуйста, ознакомьтесь с правилами работы консультантов на нашем портале.

—> Для вас всегда работает специальный раздел для нашего совместного общения и публикации новостей о работе раздела консультаций. Уделите ему внимание и посещайте время от времени. Там будут публиковаться все новости о доработках раздела и его формате работы – где вы можете задать любые интересующие вас вопросы.

—> Для экстренной связи с администрацией портала используйте нашу почту: mlab@medihost.ru

—> Спасибо за то, что вы с нами!

—> Не занимайтесь самолечением. Только ответственный подход и консультация с медицинским специалистом поможет избежать негативных последствий самолечения. Вся информация, размещенная на портале Medihost, носит ознакомительный характер и не может заменить собой посещение врача. В случае возникновения каких-либо симптомов заболевания или недомогания следует обратиться к врачу в медицинское учреждение.

—> Подбор и назначение лекарственных препаратов может только медицинский работник. Показания к применению и дозировку лекарственных веществ необходимо согласовывать с лечащим врачом.

—> Медицинский портал Medihost является информационным ресурсом и содержит исключительно справочную информацию. Материалы о различных заболеваниях и способах лечения не могут использоваться пациентами для самовольного изменения плана лечения и назначений врача.

—> Администрация портала не берет на себя ответственности за материальный ущерб, а также ущерб здоровью нанесенный в результате использования информации, размещенной на сайте Medihost.

Источник

Энтропия

(от греч. entropía — поворот, превращение)

понятие, впервые введенное в термодинамике (См. Термодинамика) для определения меры необратимого рассеяния энергии. Э. широко применяется и в других областях науки: в статистической физике (См. Статистическая физика) как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Эти трактовки Э. имеют глубокую внутреннюю связь. Например, на основе представлений об информационной Э. можно вывести все важнейшие положения статистической физики.

В термодинамике понятие «Э.» было введено Р. Клаузиусом (1865), который показал, что процесс превращения теплоты в работу следует общей физической закономерности — второму началу термодинамики (См. Второе начало термодинамики). Его можно сформулировать строго математически, если ввести особую функцию состояния — Э.

Так, для термодинамической системы, совершающей квазистатически (бесконечно медленно) циклический процесс, в котором система последовательно получает малые количества теплоты δQ при соответствующих значениях абсолютной температуры Т, интеграл от «приведенного» количества теплоты δQ/ Т по всему циклу равен нулю

( , т. н. равенство Клаузиуса).

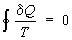
Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклический процесс как сумму очень большого, в пределе бесконечного, числа элементарных обратимых Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражение

представляло собой полный дифференциал функции состояния S, названное «Э.» (дифференциальное определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, например, значениями температур и объемов) равна

(2)

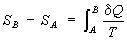
(интегральное определение Э.). Интегрирование здесь ведется вдоль пути любого квазистатического процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение Э. ΔS = S_B — S_A не зависит от пути интегрирования.

Т. о., из второго начала термодинамики следует, что существует однозначная функция состояния S, которая при квазистатических адиабатных процессах (δQ = 0) остаётся постоянной. Процессы, в которых Э. остаётся постоянной, называются изоэнтропийными. Примером может служить процесс, широко используемый для получения низких температур, — адиабатное размагничивание (см. Магнитное охлаждение). При изотермических процессах изменение Э. равно отношению сообщенной системе теплоты к абсолютной температуре. Например, изменение Э. при испарении жидкости равно отношению теплоты испарения к температуре испарения при условии равновесия жидкости с её насыщенным паром.

Согласно первому началу термодинамики (См. Первое начало термодинамики) (закону сохранения энергии), δQ = dU+pdV, т. е. сообщаемое системе количество теплоты равно сумме приращения внутренней энергии dU и совершаемой системой работы pdV, где р — давление, V — объём системы. С учётом первого начала термодинамики дифференциальное определение Э. принимает вид

, (3)

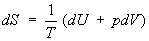
откуда следует, что при выборе в качестве независимых переменных внутренней энергии U и объёма V частные производные Э. связаны с абсолютной температурой и давлением соотношениями:

(4) и . (5)

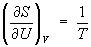
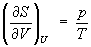
Эти выражения представляют собой уравнения состояния (См. Уравнение состояния) системы (первое — калорическое, второе — термическое). Уравнение (4) лежит в основе определения абсолютной температуры (См. Абсолютная температура) (см. также Температура, Температурные шкалы).

Формула (2) определяет Э. лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. произвольным). Абсолютное значение Э. позволяет установить Третье начало термодинамики, или Нернста теорему: при стремлении абсолютной температуры к нулю разность ΔS для любого вещества стремится к нулю независимо от внешних параметров. Поэтому: Э. всех веществ при абсолютном нуле температуры можно принять равной нулю (эту формулировку теоремы Нернста предложил в 1911 М. Планк). Основываясь на ней, за начальную точку отсчёта Э. принимают S_o = 0 при Т = 0.

Важность понятия Э. для анализа необратимых (неравновесных) процессов: также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведённой теплоты δQ / Т по замкнутому пути всегда отрицателен

( , т. н. неравенство Клаузиуса).

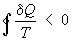
Это неравенство — следствие теоремы Карно: кпд частично или полностью необратимого циклического процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что

(6)

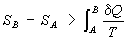
поэтому Э. адиабатически изолированной системы при необратимых процессах может только возрастать.

Т. о., Э. определяет характер процессов в адиабатической системе: возможны только такие процессы, при которых Э. либо остаётся неизменной (обратимые процессы), либо возрастает (необратимые процессы). При этом не обязательно, чтобы возрастала Э. каждого из тел, участвующего в процессе. Увеличивается общая: сумма Э. тел, в которых процесс вызвал изменения.

Термодинамическому равновесию адиабатической системы соответствует состояние с максимумом Э. Энтропия может иметь не один, а несколько максимумов, при этом система будет иметь несколько состояний равновесия. Равновесие, которому соответствует наибольший максимум Э., называется абсолютно устойчивым (стабильным). Из условия максимальности Э. адиабатические системы в состоянии равновесия вытекает важное следствие: температура всех частей системы в состоянии равновесия одинакова.

Понятие «Э.» применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамического равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но ещё макроскопических объёмах. Такие состояния можно охарактеризовать термодинамическими параметрами (температурой, давлением и т. д.), слабо зависящими от пространственных координат и времени, а Э. термодинамически неравновесного состояния определить как Э. равновесного состояния, характеризующегося теми же значениями параметров. В целом Э. неравновесной системы равна сумме Э. её частей, находящихся в локальном равновесии.

Термодинамика неравновесных процессов позволяет более детально, чем классическая термодинамика, исследовать процесс возрастания Э. и вычислить количество Э., образующейся в единице объёма в единицу времени вследствие отклонения системы от термодинамического равновесия — Производство энтропии. Производство Э. всегда положительно и математически выражается квадратичной формой от градиентов термодинамических параметров (температуры, гидродинамической скорости или концентраций компонентов смеси) с коэффициентами, называемыми кинетическими (см. Онсагера теорема).

Статистическая физика связывает Э. с вероятностью осуществления данного макроскопического состояния системы. Э. определяется через логарифм статистического веса (См. Статистический вес) Ω данного равновесного состояния

где k — Больцмана постоянная, Ω (E, N) — число квантовомеханических уровней в узком интервале энергии ΔЕ вблизи значения энергии Е системы из N частиц. Впервые связь Э. с вероятностью состояния системы была установлена Л. Больцманом в 1872: возрастание Э. системы обусловлено её переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отдельным подсистемам.

В отличие от термодинамики статистическая физика рассматривает особый класс процессов — Флуктуации, при которых система переходит из более вероятного состояния в менее вероятное, и её Э. уменьшается. Наличие флуктуаций показывает, что закон возрастания Э. выполняется только в среднем для достаточно большого промежутка времени.

Э. в статистической физике тесно связана с информационной Э., которая служит мерой неопределённости сообщений данного источника (сообщения описываются множеством величин х₁, x₂. x_n, которые могут быть, например, словами какого-либо языка, и соответствующих вероятностей p₁, p₂. p_n появления величин x₁, x₂. x_n в сообщении). Для определённого (дискретного) статистического распределения вероятностей р_к информационной Э. называют величину

(8)

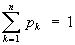
Значение Н_и равно нулю, если какое-либо из p_k равно 1, а остальные — нулю, т. е. неопределённость в информации отсутствует. Э. принимает наибольшее значение, когда p_k равны между собой и неопределённость в информации максимальна. Информационная Э., как и термодинамическая, обладает свойством аддитивности (Э. нескольких сообщений равна сумме Э. отдельных сообщений). К. Э. Шеннон показал, что Э. источника информации определяет критическое значение скорости «помехоустойчивой» передачи информации по конкретному каналу связи (см. Шеннона теорема). Из вероятностной трактовки информационной Э. могут быть выведены основные распределения статистической физики: каноническое Гиббса распределение, которое соответствует максимальному значению информационной Э. при заданной средней энергии, и большое каноническое распределение Гиббса — при заданных средней энергии и числа частиц в системе.

Понятие Э., как показал впервые Э. Шрёдингер (1944), существенно и для понимания явлений жизни. Живой организм с точки зрения протекающих в нём физико-химических процессов можно рассматривать как сложную открытую систему (См. Открытые системы), находящуюся в неравновесном, но стационарном состоянии. Для организмов характерна сбалансированность процессов, ведущих к росту Э., и процессов обмена, уменьшающих её. Однако жизнь не сводится к простой совокупности физико-химических процессов, ей свойственны сложные процессы саморегулирования. Поэтому с помощью понятия Э. нельзя охарактеризовать жизнедеятельность организмов в целом.

Э., характеризуя вероятность осуществления данного состояния системы, согласно (7) является мерой его неупорядоченности. Изменение Э. ΔS обусловлено как изменением р, V и Т, так и процессами, протекающими при р, Т = const и связанными с превращением веществ, включая изменение их агрегатного состояния, растворение и химическое взаимодействие.

Изотермическое сжатие вещества приводит к уменьшению, а изотермическое расширение и нагревание — к увеличению его Э., что соответствует уравнениям, вытекающим из первого и второго начал термодинамики (см. Термодинамика):

; (9)

; (10) . (11)

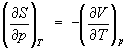
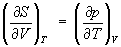
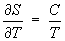
Формулу (11) применяют для практического определения абсолютного значения Э. при температуре Т, используя постулат Планка и значения теплоёмкости С, теплот и температур фазовых переходов в интервале от 0 до Т К.

В соответствии с (1) Э. измеряется в кал/(моль· К) (энтропийная единица — э. е.) и дж/(моль·К). При расчётах обычно применяют значения Э. в стандартном состоянии, чаще всего при 298,15 К (25 °С), т. е. S 0 ₂₉₈; таковы приводимые ниже в статье значения Э.

Э. увеличивается при переходе вещества в состояние с большей энергией. Δ S сублимации > ΔS парообразования >> ΔS плавления >ΔS полиморфного превращения. Например, Э. воды в кристаллическом состоянии равна 11,5, в жидком — 16,75, в газообразном — 45,11 э. е.

Чем выше твёрдость вещества, тем меньше его Э.; так, Э. алмаза (0,57 э. е.) вдвое меньше Э. графита (1,37 э. е.). Карбиды, бориды и другие очень твёрдые вещества характеризуются небольшой Э.

Э. аморфного тела несколько больше Э. кристаллического. Возрастание степени дисперсности системы также приводит к некоторому увеличению её Э.

Э. возрастает по мере усложнения молекулы вещества; так, для газов N₂О, N₂O₃ и N₂O₅ Э. составляет соответственно 52,6; 73,4 и 85,0 э. е. При одной и той же молекулярной массе Э. разветвленных углеводородов меньше Э. неразветвлённых; Э. циклоалкана (См. Циклоалканы) (циклана) меньше Э. соответствующего ему алкен (См. Алкены)а.

Э. простых веществ и соединений (например, хлоридов ACI_n), а также её изменения при плавлении и парообразовании являются периодическими функциями порядкового номера соответствующего элемента. Периодичность изменения Э. для сходных химических реакций типа 1 /_n А_крист + 1 /₂Сl_2газ = 1 /_n ACln _крист практически не проявляется. В совокупности веществ-аналогов, например АСl_4газ (А — С, Si, Ge, Sn, Pb) Э. изменяется закономерно. Сходство веществ (N₂ и СО; CdCl₂ и ZnCl₂; Ag₂Se и Ag₂Te; ВаСОз и BaSiO₃; PbWO₄ и РЬМоО4) проявляется в близости их Э. Выявление закономерности изменения Э. в рядах подобных веществ, обусловленного различиями в их строении и составе, позволило разработать методы приближённого расчёта Э.

Знак изменения Э. при химической реакции ΔS _{х. р.} определяется знаком изменения объёма системы ΔV _{х. р.}; однако возможны процессы (изомеризация, циклизация), в которых ΔS _{х. р.} ≠ 0, хотя ΔV _{х. р.} — 0. В соответствии с уравнением ΔG = ΔН — ТΔS (G — Гиббсова энергия, Н — Энтальпия) знак и абсолютное значение ΔS _{х. р.} важны для суждения о влиянии температуры на Равновесие химическое. Возможны самопроизвольные экзотермические. процессы (ΔG

Лит.: Клаузиус P., в кн.: Второе начало термодинамики, М.—Л., 1934, с. 71—158; Зоммерфельд А., Термодинамика и статистическая физика, пер. с нем., М., 1955; Майер Дж., Гепперт-Майер М., Статистическая механика, пер. с англ., М., 1952; Де Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Яглом А. М., Яглом И. М., Вероятность и информация, 3 изд., М., 1973; Бриллюен Л., Наука и теория информации, пер. с англ., М., 1959. См. также лит. при ст. Термодинамика, Термодинамика неравновесных процессов и Статистическая физика.

Источник