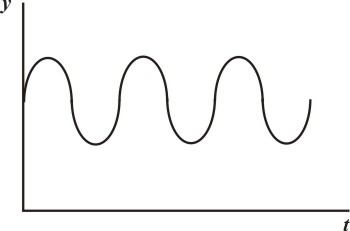
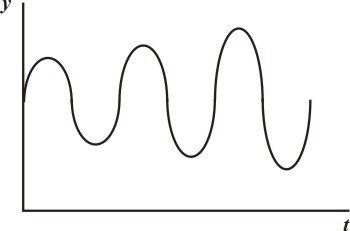
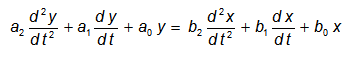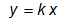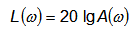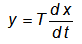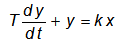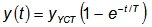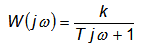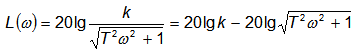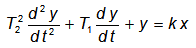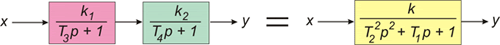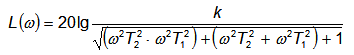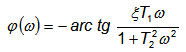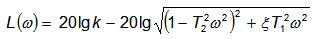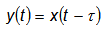график выходного сигнала колебательного звена имеет форму
3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья
Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!
Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Тема сегодняшней статьи:
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
Хочешь вкусить плодов познания? — Грызи гранит науки!
Понятие “типовые звенья” в теории управления техническими системами, в основном, связано с описанием САУ (САР) в переменных “вход – выход”, т.е. описание систем в передаточных функциях. Любую линейную САУ (САР) или линеаризованную САР можно структурно расчленить на простейшие элементы (звенья), соединенные между собой соответствующими последовательными, параллельными связями, местными и локальными обратными связями, сумматорами, сравнивающими устройствами и т.д.
Достигнуто общепринятое соглашение, что наиболее удобно расчленять структурную схему САР на звенья 1-го и 2-го порядков. Принято называть такие простейшие звенья типовыми.
С другой стороны, реальная линеаризованная (линейная) система состоит из набора отдельных узлов и агрегатов, соединенных соответствующими связями, причем порядок уравнений динамики вышеуказанных узлов и агрегатов может быть и выше второго. В этом случае звенья (узлы и агрегаты) САР можно классифицировать по их свойствам.
Различают 3 типа звеньев:
Существуют также особые звенья, которые будут рассмотрены позднее.
Учитывая, что передаточная функция линейного (линеаризованного) звена может быть записана как:
где: и
— полиномы по степеням s, причем коэффициенты при низшей степени s в полиномах
,
равны 1, классификацию на типы звеньев можно объяснить видом полиномов
или (что эквивалентно) видом коэффициентов в соответствующих уравнениях динамики звена.
Подробнее о передаточной функции см. здесь.
Позиционным звеном считают звено, в котором полиномы N(s) и L(s) содержат свободные члены (равные 1). Например:
или в уравнении динамики (x(t) – входной сигнал, y(t) – выходной):
Из типовых звеньев (1-го и 2-го порядка) к позиционным звеньям относятся: идеальное усилительное звено, апериодические звенья 1-го и 2-го порядка, колебательное звено и форсирующее звено.
Дифференцирующим звеном считается звено, в котором полином L(s) содержит свободный член (равный 1), а полином N(s) не содержит свободного члена ().
Например:
или в уравнении динамики:
Из типовых звеньев к дифференцирующим звеньям относятся идеальное дифференцирующее звено, инерционно-дифференцирующее звено.
Интегрирующим звеном считается звено, в котором полином N(s) содержит свободный член (), а полином L(s), не содержит свободного члена (
). Например:
или в уравнении динамики:
Из типовых звеньев к интегрирующим звеньям относятся идеальное интегрирующее звено, инерционно–интегрирующее звено.
Пример переходного процесса при единичном ступенчатом воздействии на три разных звена, приведенных выше:
3.2.1. Идеальное усилительное звено
Уравнение динамики каждого звена имеет вид: , т.е. уравнение не является дифференциальным, следовательно, данное звено является безынерционным.
Переходя к изображениям , получаем:
– уравнение динамики звена в изображениях.
Передаточная функция идеального усилительного звена:
АФЧХ не зависит от ω, поскольку:
Рисунок 3.2.1 АФЧХ идеального усилительного звена
Годограф АФЧХ “вырождается” в точку: U(ω) =K; V(ω) =0;
A(ω) ≡modW(iω) =│W(iω)│=K =>
Lm(ω)=20lgA(ω) =20lgK; =>
φ(ω) = const = 0 т.е. фазового сдвига нет. Следовательно, данное звено является безынерционным, чисто усилительным звеном.
Рисунок 3.2.4 ЛАХ идеального усилительного звена
Найдем весовую w(t) и переходную h(t) функции звена (подробнее см. здесь).
Весовая функция:
3.2.2. Идеальное дифференцирующее звено
Уравнение динамики звена имеет вид:
где: – постоянная времени.
Переходя к изображениям:
Уравнение динамики звена в изображениях:
Передаточная функция идеального дифференцирующего звена:
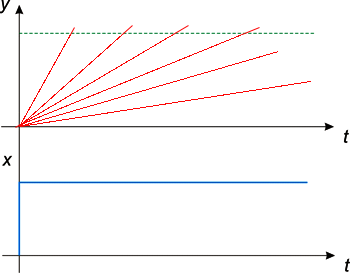
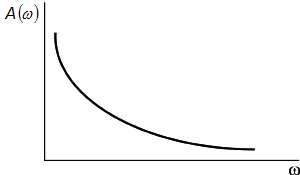
Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:
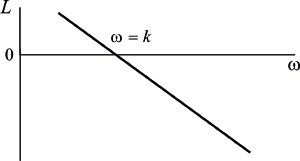
Логарифмическая амплитудная характеристика ЛАХ::
Из рисунка 3.2.9 видно, что данное звено обеспечивает опережение по фазе на /2 (при любой частоте входного сигнала).
Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.
Найдем весовую функцию звена:
Учитывая, что δ(t) имеет вид как на рис.3.2.11 (зависимость показана утрированно), а весовая функция пропорциональна производной от δ(t):
Найдем переходную функцию звена:
Иногда идеальное дифференцирующее звено представляется в виде или
. В последнем варианте коэффициент К имеет смысл постоянной времени.
3.2.3. Идеальное интегрирующее звено
Уравнение динамики такого звена имеет вид:
или в изображениях:
Передаточная функция идеального интегрирующего звена:
Умножая числитель и знаменатель на i, получаем:
Годограф АФЧХ имеет вид:
Данное звено всегда дает отставание по фазе на угол .
Найдем весовую функцию звена:
Найдем переходную функцию звена:
Примерами устройств, близких к идеальному усилительному звену, можно считать: широкополосный электронный усилитель (приближенно), механический редуктор без учета инерционности и нелинейных эффектов, жесткую механическую муфту и т.д.
Примером идеального дифференцирующего звена можно считать тахогенератор:
где u(t) – напряжение на клеммах тахогенератора, φ(t) – угол поворота якоря (ротора) тахогенератора.
Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.
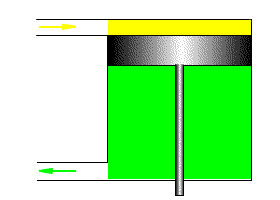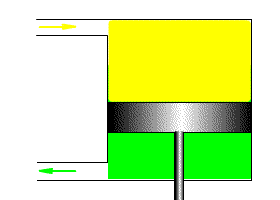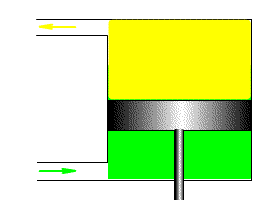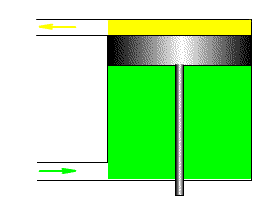
Пример интегрирующего и дифференцирующего звена на основе конденсатора
Один и тот же технический элемент, с точки зрения теории автоматического управления, может выступать как в качестве интегрирующего, так и в качестве дифференцирующего звена.
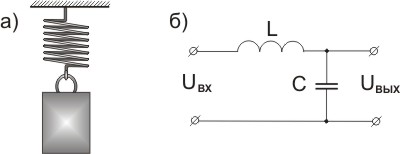
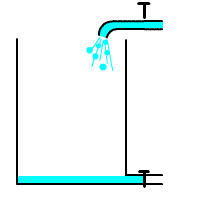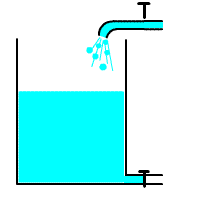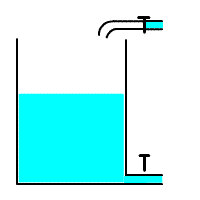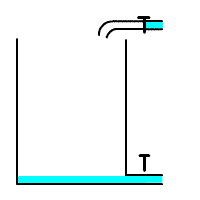
В качестве примера интегрирующего звена можно рассмотреть конденсатор, где входным воздействием является ток, а выходным результатом является напряжение на клеммах конденсатора. Действительно, при малом токе и большой емкости конденсатора, в случае ступенчатого изменения тока с 0, мы получаем график напряжения, совпадающий по форме с переходной функцией интегрирующего звена. На рисунке 3.2.20 представлена такая модель, где ток ступенькой меняется на пятой секунде расчета.
Тот же самый конденсатор, при определенных параметрах сети, может выступать в качестве идеального дифференцирующего звена, если в качестве входного воздействия подавать напряжение, а в качестве результирующей величины использовать ток в цепи.
Электрическая схема использования конденсатора в качестве дифференцирующего звена с гармоническим анализатором приведена на рисунке 3.2.22. На графиках гармонического анализатора видно, что угол наклона ЛАХ составляет 20 dB/dec, а угол сдвига фазы равен или 90 градусов на графике.
Примеры моделей, использованные в данной лекции, можно взять в этом архиве.
Типовые звенья автоматических систем



При исследовании автоматических систем первостепенное значение приобретает характер преобразования сигналов в отдельных звеньях. Динамические системы, передаточные функции которых имеют вид простых дробей, называются типовыми или элементарными. Любая промышленная автоматическая система может быть представлена в виде соединенных между собой типовых звеньев и наоборот любую автоматическую систему можно создать путем соответствующего подбора и соединения типовых звеньев.
Имеется огромное количество разнообразных систем автоматического регулирования, которые содержат различные конструктивные узлы и устройства: чувствительные элементы, усилители, исполнительные органы, объекты управления и т.д. Это объясняется тем, что звенья автоматических систем, имеющие различную конструкцию и принципы действия, использующие разные виды энергии и выполняющие разные функции, но обладают одинаковыми динамическими свойствами и описываются одинаковыми дифференциальными уравнениями.
Устройства с однотипными динамическими характеристиками
Их основу составляет звено направленного действия, основное свойство которого заключается в том, что выходная величина y(t) зависит от входной величины x(t), но обратное воздействие выхода на вход отсутствует. Любое из них может быть отнесено к одному из нескольких типов, что существенно упрощает задачу проектирования и исследования систем автоматического регулирования. Присоединение к выходу такого звена другого звена не изменяет передаточной функции первого звена. При изменении входного сигнала изменяется и выходной; если входной сигнал не меняется, то не должен изменяться и выходной сигнал. Для того чтобы элемент автоматической системы отображался звеном направленного действия, необходимо учитывать нагрузку на его выходе. При соединении звеньев направленного действия они сохраняют свои прежние свойства независимо от схемы соединения.
Физическая природа звена направленного действия может быть любой. Можно выделить шесть основных разновидностей дифференциальных уравнений не выше второго порядка, описывающих поведение тех или иных элементарных устройств автоматических систем. Использование этой методики позволило создать общую теорию автоматического регулирования.
Любую линейную автоматическую систему можно разбить на типовые динамические звенья, которые описываются обычными дифференциальными уравнениями не выше второго порядка. Не всегда один элемент автоматической системы заменяется одним звеном. Элемент может быть представлен комбинацией из нескольких типовых звеньев. Поэтому количество звеньев, составляющих анализируемую автоматическую систему, может отличаться от количества элементов этой системы.
Возможность расчленения сложной автоматической системы на элементарные звенья значительно упрощает анализ систем, так как задача составления дифференциальных уравнений автоматической системы в целом сводится к составлению уравнений отдельных звеньев. Кроме того, это позволяет представить автоматическую систему в виде структурной схемы, обеспечивая наглядность и облегчая представление о протекающих в ней процессах. Наконец, такой подход дает возможность обобщенного теоретического рассмотрения и сравнения свойств различных автоматических систем.
| Динамическим звеном, или просто звеном, называется элемент (часть) автоматической системы, который обладает определенными динамическими свойствами. |
Под типовым динамическим звеном понимается математическая модель искусственно выделяемой части автоматической системы, характеризуемая некоторым простейшим алгоритмом работы.
Одним типовым звеном иногда могут быть представлены несколько элементов автоматической системы или наоборот один элемент может быть представлен в виде нескольких звеньев.
За типовые звенья, по-видимому, целесообразно принять такие, которые могут служить основой для построения любых других звеньев и систем, встречающихся на практике. Обычно за основу принимают звено, обладающее одной степенью свободы. Математические процессы в таком звене описываются дифференциальным уравнением второго порядка.
В теории автоматического управления принята следующая форма записи уравнения: выходная величина и ее производные находятся в левой части, причем на первом месте стоит производная высшего порядка; выходная величина входит в уравнение с коэффициентом, равным единице; входная величина, а также в более общем случае ее производные и другие члены (возмущения) стоят в правой части уравнения.
Если принять это уравнение за исходное, то легко вывести уравнения различных типов звеньев. Следует подчеркнуть, что расчленение систем автоматического регулирования на типовые звенья имеет под собой не только формальную математическую, но и техническую основу. Целесообразность расчленения динамического элемента на типовые звенья объясняется особенностью технической реализации систем автоматического регулирования, состоящих обычно из совокупности сравнительно не сложных устройств направленного действия.
Так как отдельные звенья имеют различные передаточные функции, то они различаются по виду переходного процесса, который возникает при изменении входной величины. Для сравнения характеристик звеньев принято рассматривать переходный процесс при скачкообразном изменении входной величины при нулевых единичных условиях, т.е. приединичном воздействии. Такое воздействие выбрано не случайно. Для многих устройств характерны внезапные включения или выключения, скачкообразное увеличение или сброс нагрузки и тому подобные резкие изменения режима работы.
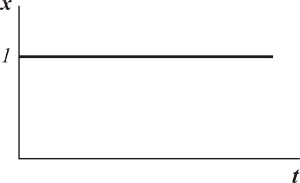
Изменение входной величины (единичное воздействие)
Функцию, определяющую изменение величины на выходе звена при этих условиях называют переходной функцией звена. Она может быть получена путем решения дифференциального уравнения относительно выходной величины при скачкообразном характере изменения входной величины или экспериментально путем записи изменения выходной величины при скачкообразном изменении входной. Эту функцию иногда называют функцией разгона.
Другое значительное упрощение методики анализа систем автоматического регулирования в использовании такого метода, который вообще не требует решения дифференциальных уравнений. В основу этого метода положена оценка реакции автоматической системы при воздействии на нее гармонического сигнала, имеющего постоянную амплитуду и частоту. Этот метод носит название частотного. Математической основой этого метода является преобразование Фурье. Частотные характеристики звеньев могут быть получены из дифференциальных уравнений звеньев или определены экспериментально.
Типовые звенья подразделяют на:
По ряду общих закономерностей типовые звенья автоматических систем можно разделить на следующие группы:
— статические звенья, у которых статическая характеристика отлична от нуля, имеет однозначную связь между входной и выходной переменными в статическом режиме. К ним относят пропорциональное, апериодическое первого порядка и колебательное звенья;
Типовые динамические звенья являются основой для построения математической модели автоматической системы любой сложности. Познакомимся с каждым типовым звеном в отдельности.
Пропорциональное звено воспроизводит без искажения и запаздывания, но с изменением масштаба, входную величину. Переходный процесс в пропорциональном звене отсутствует. В этом случае зависимость между выходной и входной величинами, как в статике, так и в динамике можно представить в виде:
Примером такого звена являются механический редуктор, безинерционный усилитель, делитель напряжения и т.п. Многие датчики сигналов также могут рассматриваться как безинерционные звенья.
 Коэффициент усиления системы равен величине отношения плеч рычага Коэффициент усиления системы равен величине отношения плеч рычага | 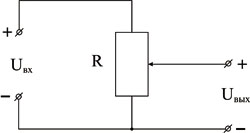 Коэффициент усиления системы равен величине отношения сопротивлений, к которым приложено выходное и входное напряжения Коэффициент усиления системы равен величине отношения сопротивлений, к которым приложено выходное и входное напряжения |
 Коэффициент усиления системы равен величине отношения количества зубьев шестерен Коэффициент усиления системы равен величине отношения количества зубьев шестерен | 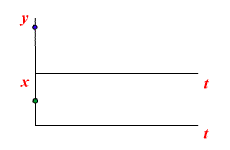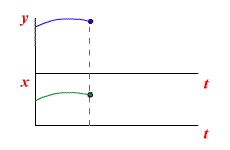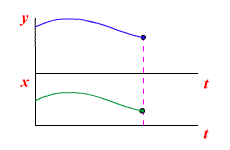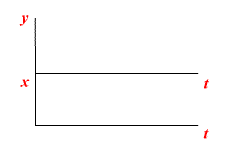 |
Примеры пропорциональных звеньев
Таким образом, передаточная функция пропорционального звена равна коэффициенту усиления
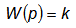 |
| Коэффициентом усиления kпропорционального звена или пропорциональной системы из нескольких звеньев называется отношение выходной величины yко входной x при разомкнутой системе в установившемся состоянии. |
Это определение коэффициента усиления справедливо для случая линейных характеристик звена или системы. Иногда коэффициент усиления называют коэффициентом пропорциональности. В случае, когда характеристики нелинейны, для определения коэффициента усиления пользуются отношением отклонений (приращений) выходной и входной величин при установившемся режиме, т.е.
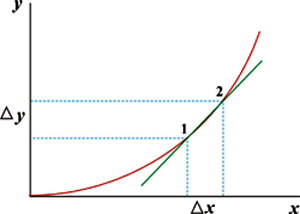 | 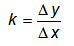 |
К определению коэффициента усиления нелинейной характеристики
Коэффициент усиления представляет собой характерную для звена и системы величину, а именно тангенс угла наклона характеристики к горизонтали. В практике автоматического регулирования коэффициент усиления может принимать следующие значения k 1.
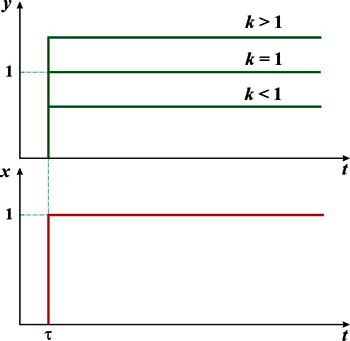
Графическое выражение переходной функции дает кривую переходного процесса. Переходный процесс в пропорциональном звене отсутствует.
Переходная характеристика пропорционального звена
Зависимость отношения амплитуд выходной и входной величин от частоты в установившемся режиме в графическом изображении представляет амплитудную частотную характеристику. Так как передаточная функция пропорционального звена не зависит от частоты, то и амплитудная частотная характеристика постоянна и равна коэффициенту усиления.
Амплитудная частотная характеристика пропорционального звена
Зависимость сдвига фазы выходной величины по отношению к входной величине при изменении частоты сигнала в установившемся режиме в графическом представлении дает фазовую частотную характеристику пропорционального звена. Так как в пропорциональном звене отсутствуют составляющие, осуществляющие накопление или рассеивание энергии, то сдвиг по фазе между входной и выходной величинами отсутствует при всех частотах.
Фазовая частотная характеристика пропорционального звена
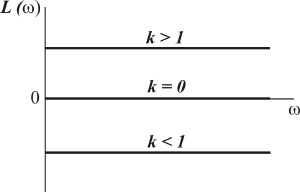
При построении характеристик звеньев используется очень широкий диапазон частот (теоретически от нуля до бесконечности), вследствие чего амплитудная частотная и фазовая частотная характеристики строятся в логарифмическом масштабе и называются логарифмическими. Для построения логарифмических частотных характеристик необходимо прологарифмировать выражение для амплитудной частотной характеристики. На практике при построении логарифмических частотных характеристик вместо натуральных логарифмов используют десятичные, выражая логарифмическую амплитудную частотную характеристику (ЛАЧХ) как
Логарифмическая амплитудная частотная характеристика пропорционального звена
Пропорциональное звено является некоторой идеализацией реальных звеньев. В действительности ни одно не в состоянии равномерно пропускать все частоты от нуля до бесконечности. Обычно к такому виду сводится одно из реальных звеньев, если можно пренебречь влиянием динамических процессов в этом звене.
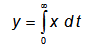
 |  |
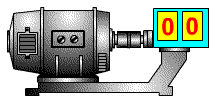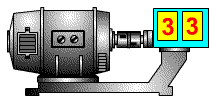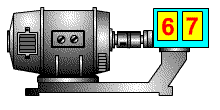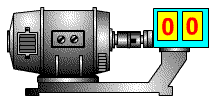 |  |
Примеры интегрирующих звеньев
Передаточная функция интегрирующего звена
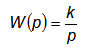 |
Если отвлечься от имеющейся иногда место ограниченности рабочего участка соответствующего элемента автоматической системы, выходная величина интегрирующего звена может неограниченно нарастать или убывать при неизменном значении входной величины. В интегрирующем звене существует определенное соотношение между значениями входной величины и скоростью изменения выходной величины. Коэффициент k характеризует соотношение между значением входной величины и скоростью изменения выходной величины. Иногда в литературе эту величину для интегрирующего звена называют постоянной времени.
Переходные характеристики интегрирующего звена
Графическое выражение переходной характеристики интегрирующего звена представляет собой прямую, проходящую через начало координат и образующую с осью абсцисс угол a = aгc tg k.
Амплитуда выходной величины интегрирующего звена тем меньше, чем больше частота 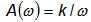
Амплитудная частотная характеристика интегрирующего звена
Интегрирующее звено создает отставание выходной величины на 90 градусов при всех частотах 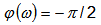
Фазовая частотная характеристика интегрирующего звена
Логарифмическая амплитудная частотная характеристика интегрирующего звена 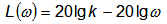
Логарифмическая амплитудная частотная характеристика интегрирующего звена
Интегрирующие звенья входят в состав интегральных, пропорционально-интегральных и пропорционально-интегрально-дифференциальных регуляторов.
Дифференцирующее звено.
Идеальным дифференцирующим звеном называется звено автоматической системы, дифференциальное уравнение которого имеет вид
Параметр Т называется постоянной времени звена или автоматической системы и служит мерой для оценки инерционности того или иного переходного процесса. Постоянная времени представляет собой величину, сочетающую в себе несколько конструктивных параметров звена или автоматической системы, определяющих накопление или рассеяние энергии внутри их. Каждый из этих параметров в отдельности может изменяться в широких пределах и потому не дает необходимой наглядности. Постоянная времени, в которую объединяются эти параметры, изменяется в более узких пределах и служит величиной, наглядно отражающей одно из органических качеств исследуемого звена или автоматической системы. В этом заключается преимущество введения понятия постоянной времени, так как удобнее оперировать одной величиной, чем несколькими.
 |  |
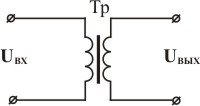 |  |
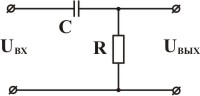
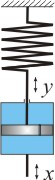
Примеры дифференцирующих звеньев
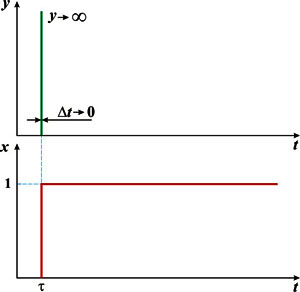
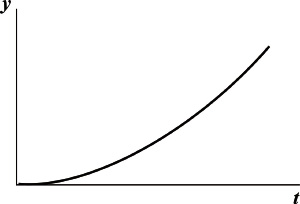
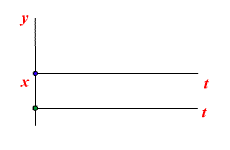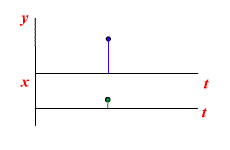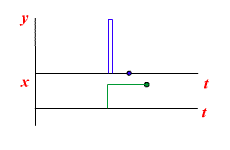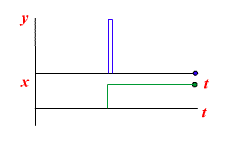
Выходная величина этого звена определяется не столько текущим значением входного воздействия, сколько скоростью его изменения (производной от входной величины). При скачкообразном изменении входной величины на выходе идеального дифференцирующего звена получается мгновенный импульс с бесконечно большой амплитудой, соответствующей бесконечно большой скорости изменения входной величины в момент скачка, а затем выходная величина принимает постоянное нулевое значение. Звено называется идеальным потому, что на практике получить импульс бесконечной амплитуды невозможно из-за ограничнности характеристик реальных автоматических систем и конечного значения мощности источников энергии.
Переходная характеристика идеального дифференцирующего звена
Передаточная функция дифференцирующего звена
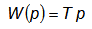 |
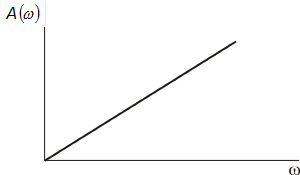
Амплитудная частотная характеристика идеального дифференцирующего звена изображена на рисунке
Амплитудная частотная характеристика дифференцирующего звена
Идеальное дифференцирующее звено создает постоянное опережение по фазе приближающееся к 90 градусам.
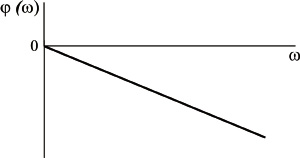
Фазовая частотная характеристика идеального дифференцирующего звена
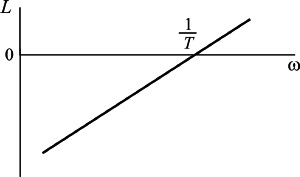
Логарифмическая амплитудная частотная характеристика идеального дифференцирующего звена приведена на рисунке
Логарифмическая амплитудная частотная характеристика дифференцирующего звена
Наличие идеального дифференцирующего звена в основном контуре системы автоматического регулирования означает введение производной в закон регулирования и обычно бывает полезно для улучшения качества регулирования и обеспечения устойчивости автоматической системы.
Апериодическое звено первого порядка.
Понятием апериодического звена объединяют такие устройства, в которых выходная величина после подачи на вход единичного воздействия изменяется монотонно, достигая некоторого установившегося значения в течение определенного времени. Такие устройства можно рассматривать как два соединенных между собой элемента, один из которых способен запасать энергию или вещество, а второй создает сопротивление перемещению энергии или вещества.
В качестве примеров апериодических звеньев первого порядка можно рассматривать двигатель любого типа (электрический, гидравлический, пневматический), механические характеристики которого (зависимость крутящего момента от частоты вращения) могут быть представлены в виде параллельных прямых. Апериодическими звеньями первого порядка являются пневматические резервуары, любые электрические RC- и RL-цепи и т.д.
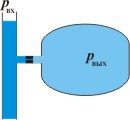 | 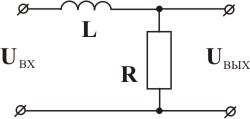 |
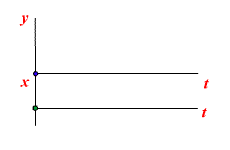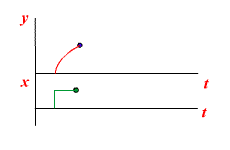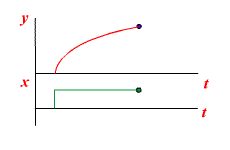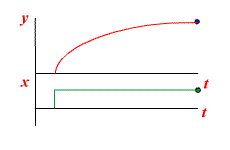 | 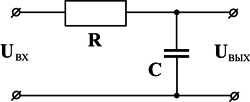 |
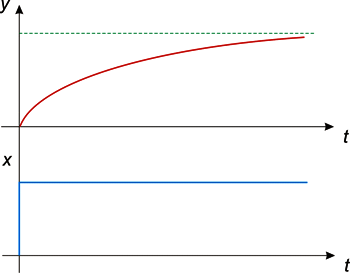
Дифференциальное уравнение апериодического звена может быть записано так
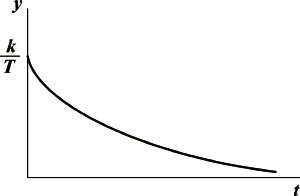
Переходная функция апериодического звена первого порядка определяется выражением
и представляет собой экспоненциальную зависимость.
Переходная характеристика апериодического звена первого порядка
Передаточная функция апериодического звена
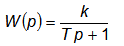 |
Из графика переходного процесса апериодического звена можно найти значение коэффициента усиления k и постоянной времени Т. Величина коэффициента усиления определяется аналогично тому, как это было описано для пропорционального звена. Постоянная времени Т апериодического звена численно равна отрезку времени, за который выходная величина, изменяясь от 0, достигнет 63 % от установившегося значения. Для большинства практических случаев исследования апериодических звеньев первого порядка можно считать, что переходный процесс в нем заканчивается к моменту времени t = 3Т. Это дает возможность экспериментального определения постоянных времени объектов, динамические свойства подобны апериодическим звеньям. Для этого экспериментально снимают график переходного процесса, если он представляет экспоненциальную зависимость или близкую к ней, то поделив время переходного процесса на три получаем экспериментальной значение постоянной времени звена или автоматической системы в целом.
Частотные характеристики апериодического звена первого порядка могут быть получены из выражения для передаточной функции путем формальной замены аргумента р аргументом jw
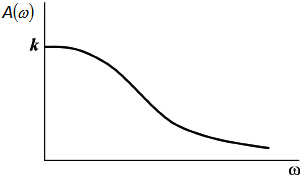
Модуль этой функции представляет собой амплитудную частотную характеристику апериодического звена первого порядка.
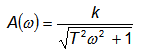
которая представлена на рисунке
Амплитудная частотная характеристика апериодического звена первого порядка
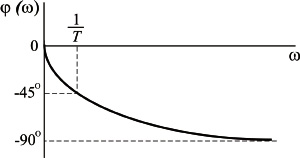
Аргумент этой функции 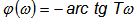
Фазовая частотная характеристика апериодического звена первого порядка
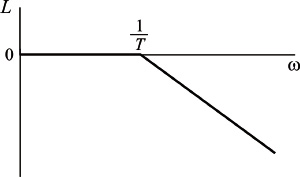
Логарифмическая амплитудная частотная характеристика апериодического звена первого порядка определяется из выражения
и приведена на рисунке
Логарифмическая амплитудная частотная характеристика апериодического звена первого порядка при k = 1
Легко понять, что каждое слагаемое этого выражения есть либо прямая линия, либо асимптотически приближается к прямым линиям при устремлении частоты к нулю и к бесконечности. Наклон аппроксимирующих прямых всегда кратен 20 дБ за декаду.
Апериодическое звено второго порядка.
Дифференциальное уравнение апериодического звена второго порядка имеет вид
Переходная характеристика апериодического звена второго порядка строится как сумма переходных характеристик последовательно соединенных звеньев
Примером апериодического звена второго порядка может служить электродвигатель постоянного тока при отсутствии момента сопротивления на валу и при учете переходных процессов в цепи якоря.
Построение ЛАЧХ для данного звена производится аналогично тому, как это было сделано для апериодического звена первого порядка по выражению
Колебательное звено.
Под колебательным звеном понимают такие устройства, в которых выходная величина после подачи на их вход единичного воздействия стремится к установившемуся значению, совершая колебания. Такие устройства должны содержать два элемента, способные запасать энергию или вещество и обмениваться этими запасами через третий элемент, создающий сопротивление перетеканию энергии или вещества.
Примерами колебательных звеньев могут служить RLC-цепи, упругие механические передачи для передачи поступательного или вращательного движения и т.п.
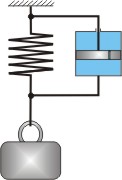 | 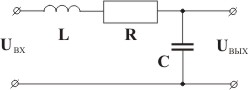 |
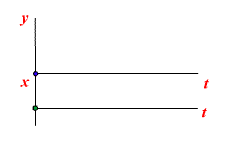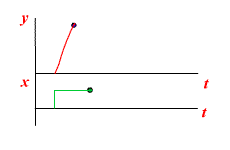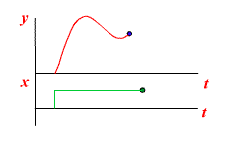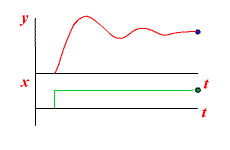 |
Примеры колебательных звеньев
Дифференциальное уравнение устойчивого колебательного звена в классической форме
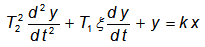
Передаточная функция устойчивого колебательного звена:
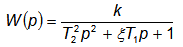 |
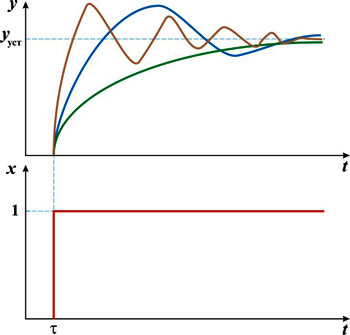
Переходная характеристика устойчивого колебательного звена при различных значениях сочеиания постоянных времениT1 и Т2 представлена на рисунке
Переходные характеристики устойчивого колебательного звена
Частотные характеристики устойчивого колебательного звена могут быть получены из выражения для передаточной функции путем формальной замены аргумента р аргументом jw
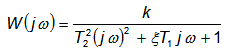
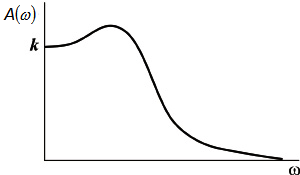
Модуль этой функции представляет собой амплитудную частотную характеристику устойчивого колебательного звена
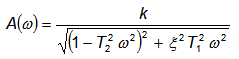
которая представлена на рисунке
Амплитудная частотная характеристика устойчивого колебательного звена
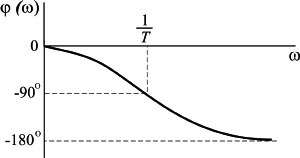
Аргумент этой функции
является фазовой частотной характеристикой колебательного звена.
Фазовая частотная характеристика колебательного звена
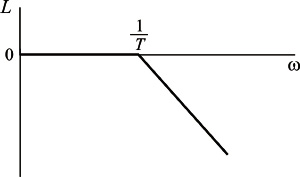
Логарифмическая амплитудная частотная характеристика колебательного звена вычисляется по выражению
и приведена на рисунке
Логарифмическая амплитудная частотная характеристика колебательного звена при k = 1
Если коэффициент x равен нулю (отсутствует рассеяние энергии), то передаточная функция колебательного звена имеет вид
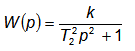 |
Систему, имеющую такую передаточную функцию, называют консервативной. Такая система не рассеивает энергии и в ней протекают незатухающие колебания.
Переходная характеристика консервативного колебательного звена
Рассмотренные выше варианты звеньев второго порядка относятся к устойчивым или звеньям с самовыравниванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся значению при ограниченном изменении входной величины или возмущающего воздействия. Термин самовыравнивание обычно применяется для звеньев, представляющих собой объекты регулирования.
Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени.
Если один из коэффициентов в знаменателе отрицателен, то колебания выходной величины с течением времени возрастают.
Передаточная функция такого звена имеет вид:
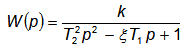 |
Такое звено называют неустойчивым колебательным звеном
Переходная характеристика неустойчивого колебательного звена
Звено запаздывания.
Под звеном с постоянным запаздыванием объединяются такие устройства, у которых выходная величина воспроизводит без искажения все изменения входной величины с некоторым постоянным запаздыванием t. Исходя из этого определения, уравнение такого звена:
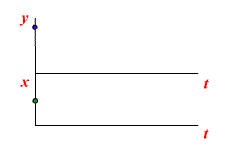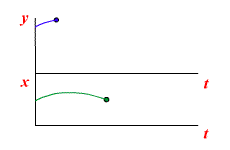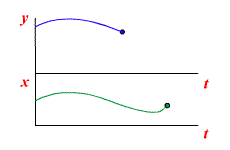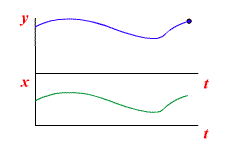 |
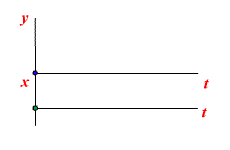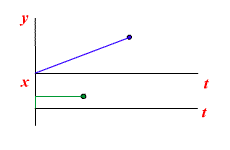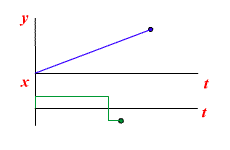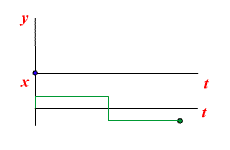
Работа звена с постоянным запаздыванием
Передаточная функция звена с постоянным запаздыванием
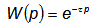 |
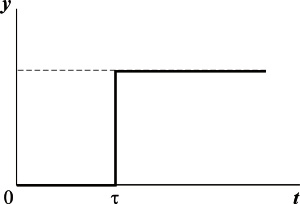
Переходная характеристика звена с постоянным запаздыванием представлена на рисунке
Переходная характеристика звена с постоянным запаздыванием
Амплитудная частотная характеристика 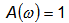
Амплитудная частотная характеристика звена запаздывания
Фазовая частотная характеристика звена с постоянным запаздыванием
Идеальные и реальные звенья.
Рассмотренные интегрирующее и дифференцирующее звенья называются идеальными. Некоторые элементы систем автоматического регулирования имеют передаточные функции
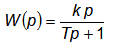 | 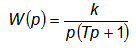 |
Такие звенья называются соответственно реальным дифференцирующим и реальным интегрирующим звеном.
Примерами реальных дифференцирующих звеньев является дифференцирующая RC- цепочка или гидравлическое изодромное устройство. Электродвигатель постоянного тока при учете электромеханической постоянной времени является реальным интегрирующим звеном. Наличие выражения (Тр + 1) в знаменателе передаточных функций реальных звеньев указывает на инерционность процессов дифференцирования и интегрирования, влияние которой легко усмотреть по переходным характеристикам идеальных и реальных звеньев. Поэтому иногда реальные дифференцирующие и интегрирующие звенья называют соответственно инерционно-дифференцирующим иинерционно-интегрирующим.
Переходная характеристика инерционно-дифференцирующего звена
Переходная характеристика инерционно-интегрирующего звена
Строго говоря, реальные звенья не являются типовыми, так как они могут быть представлены комбинацией нескольких типовых звеньев. Однако они потверждают существенные различия между идеальными и реальными процессами, происходящими в элементах автоматической системы.