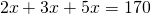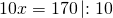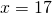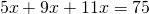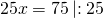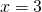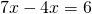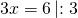как делить число в отношении дробей

Как разделить число в отношении

Как разделить число на части в данном отношении? Рассмотрим, как это сделать, на конкретных примерах.

1) Разделить число 170 на три части в отношении 2:3:5.

1)2+3+5=10 (частей) составляет все число.

2)170:10=17 — приходится на одну часть.

3)2∙17=34 — величина I части.

4)3∙17=51 — величина II части.

5)5∙17=85 — величина III части.

Пусть х — величина одной части. Поскольку мы делим число на пропорциональные части, величину одной части называют коэффициентом пропорциональности. Поэтому чаще всего сражу же пишут: пусть х — коэффициент пропорциональности. Тогда I часть равна 2х, II — 3х, III — 5х. Сумма трех частей равна числу:

Значит, I часть равна 2∙17=34, 3∙17=51, II — 3∙17=51, III — 5∙17=85.

2) Периметр треугольника равен 75 см, а стороны относятся как 5:9:11. Найти стороны треугольника.

Пусть х- коэффициент пропорциональности. Тогда стороны треугольника равны 5 см, 9х см и 11х см. По условию, периметр треугольника равен 75 см. Составим и решим уравнение:

Следовательно, стороны треугольника равны 5∙3=15 см, 9∙3=27 см, 11∙3=33 см.

Ответ: 15 см, 27 см, 33 см.

3) Настя и Лиза поделили конфеты в отношении 4:7. При этом у Лизы оказалось на 6 конфет больше. Сколько конфет было всего?

Пусть х — коэффициент пропорциональности. Тогда Насте досталось 4х конфет, Лизе — 7х конфет. Так как у Лизы конфет на 6 больше, чем у Насти, составляем уравнение:

Значит, количество конфет Насти 4∙2=8, Лизы — 7∙2=14, а всего у них 8+14=22 конфеты.

4 Comments

Решение последней (3й) задачи следует поправить, так в ней спрашивается общее количество конфет — 22.

Геннадий, спасибо, исправила.

Наверное, отношение стоимости 5 ручек к стоимости 4 тетрадей. 5 ручек стоят 5∙40=200 рублей, 4 тетради — 4∙70=280 рублей. Следовательно, отношение стоимости 5 ручек к стоимости 4 тетрадей равно 200/280=5/7.

Источник

Пропорциональное деление

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.

Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:

Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.

90 : (1 + 2 + 3) = 90 : 6 = 15;

Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.

Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:

значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то

Второй способ: обозначим искомые части буквами a, b и c:

Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:

Следовательно, c равно:

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

так как 15 + 10 + 8 = 33, то

Деление на части, обратно пропорциональные числам

Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как

Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

Источник

Деление дробей: теория и практика

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дроби

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Две дроби a/b и c/d называются равными, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число:

2. На ноль делить нельзя.

3. Когда делим ноль на любое число, всегда получаем ноль:

4. Когда делим любое число на само себя получаем единичку:

5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:

6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:

7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:

Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

Деление на смешанное число

Для деления смешанных чисел необходимо:

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Деление числа в данном отношении + задачи с решением

В шестом классе изучается тема деления чисел в данном отношении. Тема для учеников не всегда понятна с первого объяснения учителя, поэтому разберем ее подробнее на страницах сайта 7 гуру. Напишем понятия и правила, разберем примеры решения задач на деление в данном отношении.

Понятие отношения

Частное двух не равных нулю чисел a и b называется отношением чисел a и b. Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Задача 1. Разделите между двумя друзьями 80 конфет в отношении 1:4.

1 способ:
Таким способом мы решали подобные задачи в начальной школе. Сначала узнаем, сколько всего частей в целом. Узнаем количество предметов в одной части. Умножаем на нужные количества частей, чтобы ответить на вопрос.

2 способ:
Решаем по правилу деления числа на части. Этим способом предпочтительнее пользоваться при решении подобных задач.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Задача 2. Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Задача 3. Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Задача 4. Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Задача 5. Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Так как время преодоления расстояния мотоциклистом и велосипедистом равно 12:4, значит, скорость мотоциклиста будет в 3 раза больше, чем велосипедиста. Следовательно, за одно и то же время мотоциклист проедет в 3 раза большее расстояние. Это значит, что весь путь делится между ними в отношении 1:3.

Задача 6. Сортировка элементов по категориям. Поставьте в соответствующие столбцы (1:4; 2:5) числа, которые можно разделить нацело в заданных отношениях. Варианты ответов: 25, 13, 14, 45, 28, 6.

Для решения нужно сначала посчитать сумму частей первого столбца:
1 + 4 = 5
Затем проверить, какие из чисел кратны 5. Это 25 и 45.
Аналогично для второго столбца.
2 + 5 = 7
Числа, кратные 7: 14 и 28.

Источник