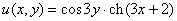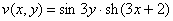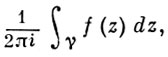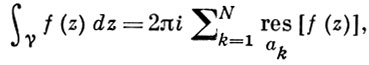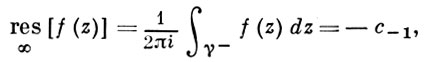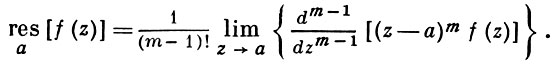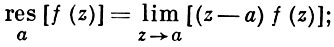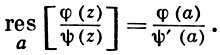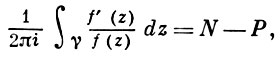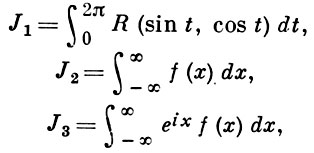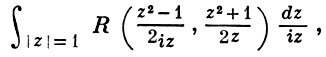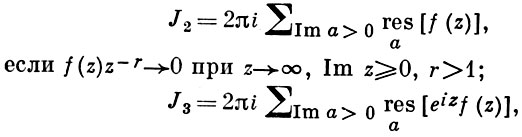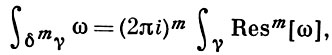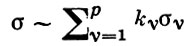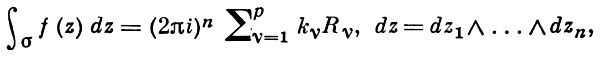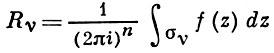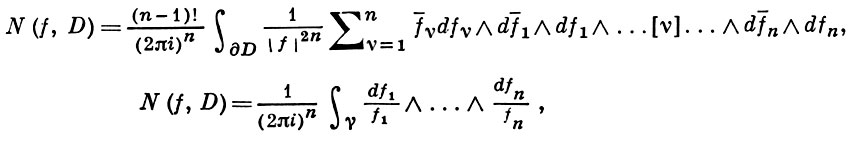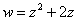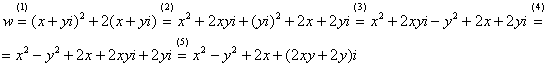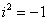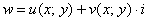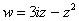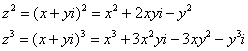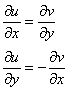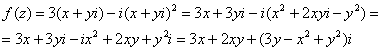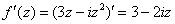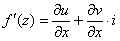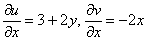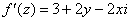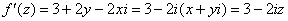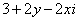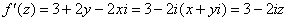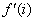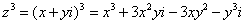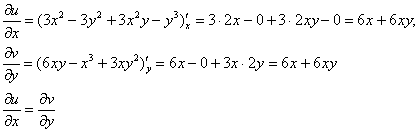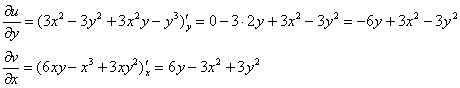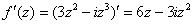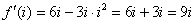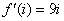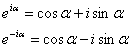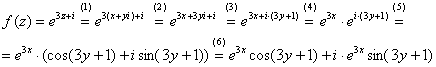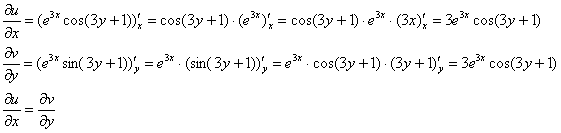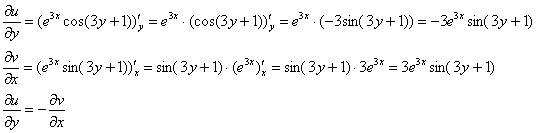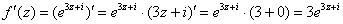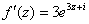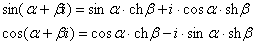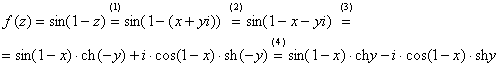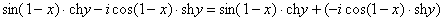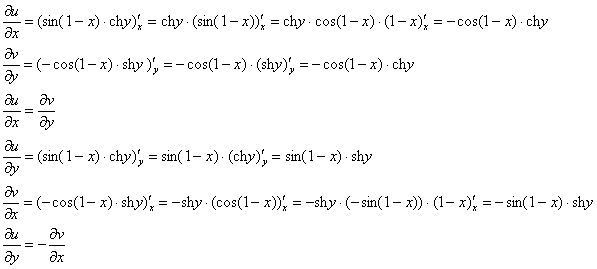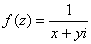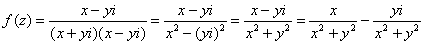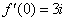как найти вычеты функции комплексной переменной
Как найти вычеты функции комплексной переменной
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z0) для z0, принадлежащей области комплексных чисел:
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
ПРИМЕР 4. Вычисление вычета в простом полюсе.
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Вычеты. Основная теорема о вычетах
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г).
Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0.
Возможно вам будут полезны данные страницы:
Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z).
Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z.
При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность \z\ = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го).
И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z
Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо.
Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f Вычислить интеграл Полюсами (конечными) подынтегральной функции являются корни zt уравнения гя = —1, которые все лежат внутри окружности В окрестности точки г = оо функция /(z) имеет следующее разложение: ИЗ КОТОРОГО ВИДНО, ЧТО В силу теоремы 6.2. Приложение вычетов к вычислению определенных интегралов. Интегралы от рациональных функций Теорема 24. Пусть f(x) — рациональная функция, т. е. где — многочлены степеней пит соответственно. Пример 6. Вычислить интеграл Применяя подстановку z = е,г. после простых преобразований (см. формулы (II)) получим, что Внутри единичного круга при условии находится только один полюс (второго порядка) Вычет функции Интегралы вида гдеД(х) — правильная рациональная дробь, а > 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при \ стремится к нулю равномерно относительно arg z. где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией. Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0): Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z\ = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43. Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку. Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой При m = 1 (простой полюс) эта формула принимает вид если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как т. е. к вычислению В.; если f(z) удовлетворяет условиям Жордана леммы. Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др. Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда. — разложение σ по этой базе, то обобщение теоремы о В. имеет вид Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975. Данная статья открывает серию уроков, на которых я рассмотрю типовые задачи, связанные с теорией функций комплексной переменной. Для успешного освоения примеров необходимо обладать базовыми знаниями о комплексных числах. В целях закрепления и повторения материала достаточно посетить страницу Комплексные числа для чайников. Также потребуются навыки нахождения частных производных второго порядка. Вот они какие, эти частные производные… даже сам сейчас немного удивился, насколько часто встречаются… Тема, которую мы начинаем разбирать, не представляет особых сложностей, и в функциях комплексной переменной, в принципе, всё понятно и доступно. Главное, придерживаться основного правила, которое выведено мной опытным путём. Читайте дальше! Сначала освежим знания о школьной функции одной переменной: Функция одной переменной В комплексном случае функциональная зависимость задается аналогично: Однозначная функция комплексной переменной Чем отличается функция комплексной переменной? Главное отличие: числа комплексные. Я не иронизирую. От таких вопросов нередко впадают в ступор, в конце статьи историю прикольную расскажу. На уроке Комплексные числа для чайников мы рассматривали комплексное число в виде Функцию комплексной переменной можно записать в виде: Функция То есть, функция комплексной переменной Найти действительную и мнимую часть функции Решение: Независимая переменная «зет», как вы помните, записывается в виде (1) В исходную функцию (2) Для первого слагаемого использовали формулу сокращенного умножения (3) Аккуратно возвели в квадрат (4) Перегруппировка слагаемых: сначала переписываем слагаемые, в которых нет мнимой единицы (первая группа), затем слагаемые, где есть (5) У второй группы выносим В результате наша функция оказалась представлена в виде Ответ: Что это получились за функции? Самые что ни на есть обыкновенные функции двух переменных, от которых можно найти такие популярные частные производные. Без пощады – находить будем. Но чуть позже. Кратко алгоритм прорешанной задачи можно записать так: в исходную функцию подставляем Найти действительную и мнимую часть функции Это пример для самостоятельного решения. Перед тем как с шашками наголо броситься в бой на комплексной плоскости, позвольте дать самый важный совет по теме: БУДЬТЕ ВНИМАТЕЛЬНЫ! Внимательным нужно быть, конечно, везде, но в комплексных числах следует быть внимательным, как никогда! Помните, что Полное решение и ответ в конце урока. Чтобы дальше легче жилось, обратим внимание на пару полезных формул. В Примере 1 было выяснено, что Теперь куб. Используя формулу сокращенного умножения Рекомендую переписать в тетрадь две рабочие формулы: Формулы очень удобно использовать на практике, поскольку они значительно ускоряют процесс решения. У меня есть две новости: хорошая и плохая. Начну с хорошей. Для функции комплексной переменной Плохая новость состоит в том, что для многих функций комплексной переменной производной не существует вообще, и приходится выяснять, дифференцируема ли та или иная функция. А «выяснять», как чует ваше сердце, связано с дополнительными заморочками. Рассмотрим функцию комплексной переменной 1) Чтобы существовали частные производные первого порядка 2) Чтобы выполнялись так называемые условия Коши-Римана: Только в этом случае будет существовать производная! Определить действительную Решение раскладывается на три последовательных этапа: 1) Найдём действительную и мнимую часть функции. Данное задание было разобрано в предыдущих примерах, поэтому запишу без комментариев: Так как Таким образом: Остановлюсь еще на одном техническом моменте: в каком порядке записывать слагаемые в действительной и мнимой частях? Да, в принципе, без разницы. Например, действительную часть можно записать так: 2) Проверим выполнение условий Коши-Римана. Их два. Начнем с проверки условия Несомненно, приятная новость – частные производные почти всегда очень простые. Проверяем выполнение второго условия Условия Коши-Римана выполнены, следовательно, функция дифференцируема. 3) Найдём производную функции. Производная тоже очень простая и находится по обычным правилам: Мнимая единица при дифференцировании считается константой. Ответ: Существуют еще два способа нахождения производной, они, конечно, применяются реже, но информация будет полезна для понимания второго урока – Как найти функцию комплексной переменной? Производную можно найти по формуле: В данном случае: Таким образом Предстоит решить обратную задачу – в полученном выражении нужно вычленить Обратное действие, как многие заметили, выполнять несколько труднее, для проверки всегда лучше взять выражение Зеркальная формула для нахождения производной: Определить действительную Краткое решение и примерный образец чистового оформления в конце урока. Всегда ли выполняются условия Коши-Римана? Теоретически они чаще не выполняются, чем выполняются. Но в практических примерах я не припомню случая, чтобы они не выполнялись =) Таким образом, если у вас «не сошлись» частные производные, то с очень большой вероятностью можно сказать, что вы где-то допустили ошибку. Усложним наши функции: Определить действительную Решение: Алгоритм решения полностью сохраняется, но в конце добавится новый пунктик: нахождение производной в точке. Для куба нужная формула уже выведена: Определим действительную и мнимую часть данной функции: Внимание и еще раз внимание! Так как Проверим выполнение условий Коши-Римана: Проверка второго условия: Получилось одно и то же, но с противоположными знаками, то есть условие Условия Коши-Римана выполнены, следовательно, функция является дифференцируемой: Вычислим значение производной в требуемой точке: Ответ: Функции с кубами встречаются часто, поэтому пример для закрепления: Определить действительную Решение и образец чистового оформления в конце урока. В теории комплексного анализа определены и другие функции комплексного аргумента: экспонента, синус, косинус и т.д. Данные функции обладают необычными и даже причудливыми свойствами – и это действительно интересно! Очень хочется рассказать, но здесь, так уж получилось, не справочник или учебник, а решебник, поэтому я рассмотрю ту же задачу с некоторыми распространенными функциями. Сначала о так называемых формулах Эйлера: Для любого действительного числа Тоже можете переписать в тетрадь в качестве справочного материала. Строго говоря, формула всего одна, но обычно для удобства пишут и частный случай с минусом в показателе. Параметр Определить действительную Решение: Генеральная линия партии остаётся непоколебимой – необходимо выделить действительную и мнимую часть функции. Приведу подробное решение, и ниже закомментирую каждый шаг: Поскольку (1) Подставляем (2) После подстановки нужно выделить действительную и мнимую часть сначала в показателе экспоненты. Для этого раскрываем скобки. (3) Группируем мнимую часть показателя, вынося мнимую единицу за скобки. (4) Используем школьное действие со степенями. (5) Для множителя (6) Раскрываем скобки, в результате: Дальнейшие действия стандартны, проверим выполнение условий Коши-Римана: Частные производные опять не очень сложные, но на всякий пожарный расписал их максимально подробно. Проверяем второе условие: Условия Коши-Римана выполнены, найдём производную: Ответ: На вторую формулу Эйлера задание для самостоятельного решения: Определить действительную Полное решение и ответ в конце урока. Непосредственно из формул Эйлера можно вывести формулу разложения синуса и косинуса на действительную и мнимую часть. Сам вывод достаточно занудный, вот он, кстати, у меня в учебнике перед глазами (Бохан, Математический анализ, том 2). Поэтому сразу приведу готовый результат, который опять полезно переписать к себе в справочник: Параметры «альфа» и «бета» принимают только действительные значения, в том числе они могут быть сложными выражениями, функциями действительной переменной. Кроме того, в формуле нарисовались гиперболические функции, при дифференцировании они превращаются друг в друга, не случайно я включил их в таблицу производных. Определить действительную Решение: Алгоритм решения очень похож на предыдущие два примера, но есть очень важные моменты, поэтому начальный этап я опять закомментирую пошагово: Поскольку 1) Подставляем (2) Сначала выделяем действительную и мнимую часть внутри синуса. В этих целях раскрываем скобки. (3) Используем формулу (4) Используем чётность гиперболического косинуса: В итоге: Внимание! Знак «минус» относится к мнимой части, и его ни в коем случае не теряем! Для наглядной иллюстрации полученный выше результат можно переписать так: Проверим выполнение условий Коши-Римана: Условия Коши-Римана выполнены. Ответ: С косинусом, дамы и господа, разбираемся самостоятельно: Определить действительную Я специально подобрал примеры посложнее, поскольку с чем-нибудь вроде Ну и в заключение рассмотрю ещё один интересный пример, когда комплексный аргумент находится в знаменателе. Пару раз в практике встречалось, разберём что-нибудь простое. Эх, старею… Определить действительную Решение: Снова необходимо выделить действительную и мнимую часть функции. Возникает вопрос, что же делать, когда «зет» находится в знаменателе? Всё бесхитростно – поможет стандартный приём умножения числителя и знаменателя на сопряженное выражение, он уже применялся в примерах урока Комплексные числа для чайников. Вспоминаем школьную формулу Вот и всё, а вы боялись: Повторюсь в третий раз – не теряем минус у мнимой части. Проверим выполнения условий Коши-Римана. Надо сказать, частные производные здесь не то чтобы о-го-го, но уже не из простейших: Ответ: В качестве эпилога короткая история про ступор, или о том, какие вопросы преподавателей являются самыми сложными. Самые сложные вопросы, как ни странно – это вопросы с очевидными ответами. А история такова: сдаёт человек экзамен по алгебре, тема билета: «Следствие основной теоремы алгебры». Экзаменатор слушает-слушает, а потом вдруг спрашивает: «А откуда это следует?». Вот это был ступор, так ступор. Вся аудитория уже угорала, но студент так и не сказал правильного ответа: «из основной теоремы алгебры». Вспоминаю историю и из личного опыта, сдаю физику, что-то там про давление жидкости, что уже не помню, но рисунок остался в памяти навсегда – изогнутая труба, по которой текла жидкость. Ответил я билет «на отлично», причем даже сам понял, что ответил. И вот преподаватель напоследок спрашивает: «Где здесь трубка тока?». Крутил-вертел я этот чертёж с изогнутой трубой минут пять, высказывал самые дикие версии, пилил трубу, рисовал какие-то проекции. А ответ был прост, трубка тока – это вся труба. Неплохо разгрузились, до встречи на уроке Как найти функцию комплексной переменной? Там разобрана обратная задача. Иногда очевидное – это самое сложное, всем желаю не тормозить! Пример 2: Решение: так как Пример 4: Решение: Так как Пример 6: Решение: определим действительную и мнимую часть данной функции. Пример 8: Решение: Так как Пример 10: Решение: Так как Автор: Емелин Александр (Переход на главную страницу)Пример 4:
Пример 5:
Тогда для любого положитыьного а ВЫЧЕТ
Функции комплексной переменной.
Дифференцирование функций комплексной переменной.
Условия Коши-РиманаПонятие функции комплексной переменной
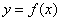
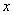
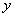
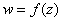
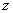
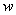
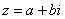
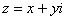
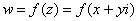
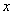
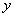
Действительная и мнимая часть функции комплексной переменной
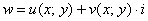
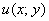
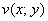
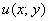
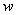
Функция 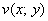
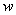
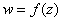
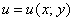
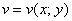
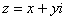
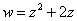
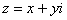
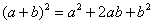
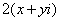
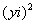
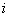
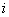
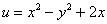
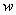
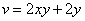
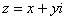
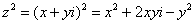
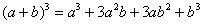
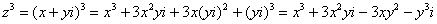
Дифференцирование функций комплексной переменной.
Условия Коши-Римана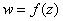
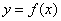
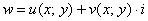
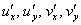
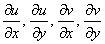
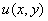
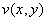
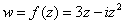
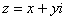
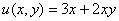
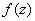
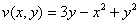
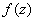
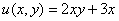
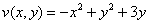
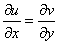
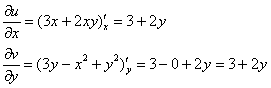
Таким образом, условие 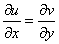
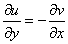
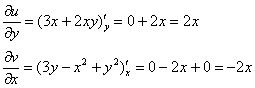
Получилось одно и то же, но с противоположными знаками, то есть, условие 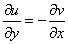
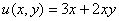
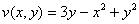
Условия Коши-Римана выполнены, 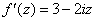
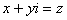
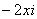
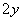
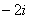
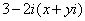
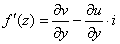
В данном случае: 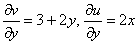
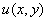
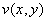
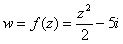
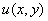
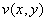
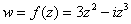
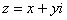
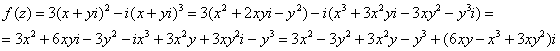

Таким образом:
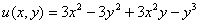
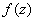
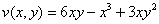
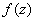
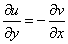
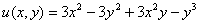
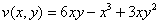
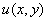
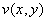
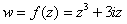
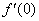
Формулы Эйлера
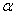
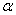
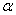
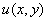
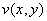
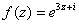
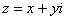
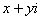
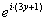
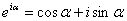
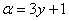
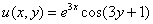
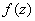
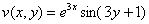
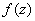
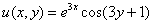
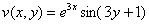
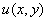
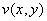
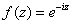
! Внимание! Знак «минус» в формуле Эйлера 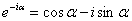
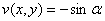
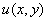
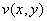
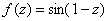
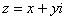
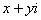
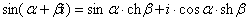
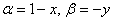
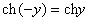
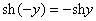
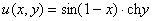
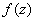
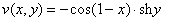
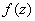
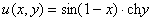
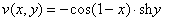
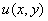
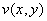
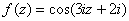
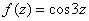
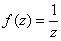
Если 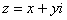
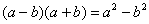
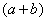
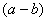
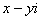
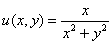
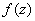
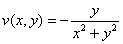
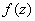
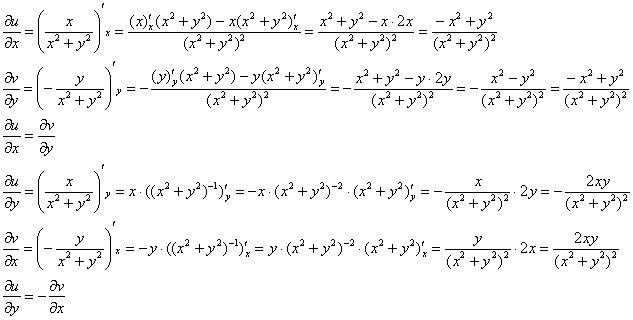
Условия Коши-Римана выполнены.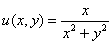
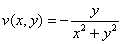
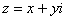
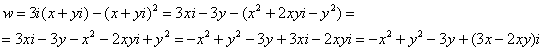
Ответ: 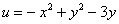
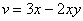
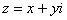
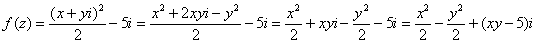
Таким образом:
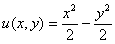
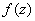
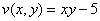
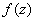
Проверим выполнение условий Коши-Римана: 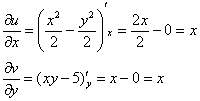
Условие 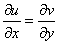
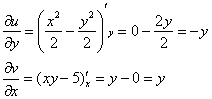
Условие 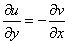
Условия Коши-Римана выполнены, найдём производную: 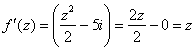
Ответ: 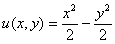
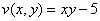
Условия Коши-Римана выполнены, 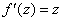
Так как 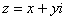
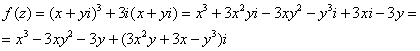
Таким образом:
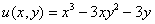
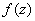
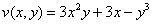
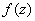
Проверим выполнение условий Коши-Римана: 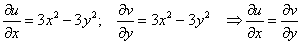
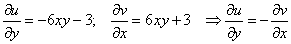
Условия Коши-Римана выполнены. 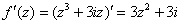
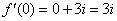
Ответ: 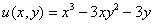
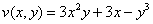
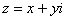
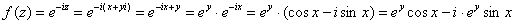
Таким образом:
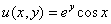
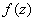
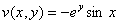
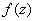
Проверим выполнение условий Коши-Римана: 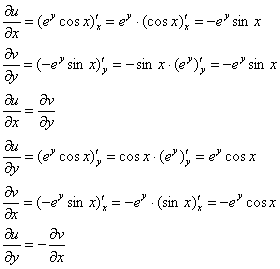
Условия Коши-Римана выполнены, найдём производную: 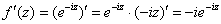
Ответ: 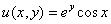
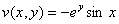
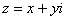
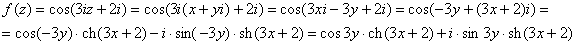
Таким образом:
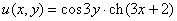
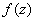
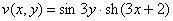
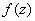
Проверим выполнение условий Коши-Римана: 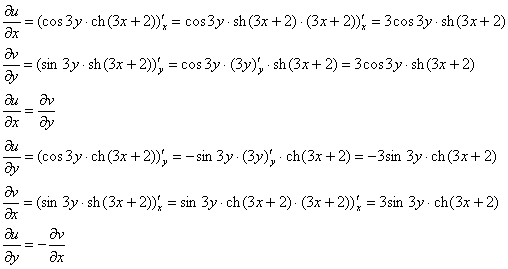
Условия Коши-Римана выполнены.
Ответ: