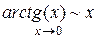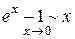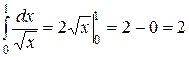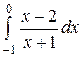Что такое эталонный интеграл
Конев В.В. Несобственные интегралы

 имеет единственную особенность во внутренней точке
имеет единственную особенность во внутренней точке  промежутка [a,b]. Составим сумму
промежутка [a,b]. Составим суммуи выполним предельный переход, устремив к нулю 

Если существует двойной предел выражения (1), не зависящий от способа предельного перехода, то он называется несобственным интегралом от функции f(x) по промежутку [a,b]:
Если предел (2) существует лишь при согласованном предельном переходе, а именно когда

В таких случаях говорят, что интеграл 
Обозначение “V.p.” введено Коши и представляет собой аббревиатуру, которая берет свое начало от слов “Valeur principale”, означающих по-французски “Главное значение”.
Любой сходящийся несобственный интеграл существует и в смысле главного значения. Обратное утверждение является неверным.
Отметим, что интегралы в смысле главного значения играют важную роль в различных приложениях. Например, интегральный логарифм определяется формулой
Исследование несобственных интегралов на сходимость.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ: ИХ ВЫЧИСЛЕНИЕ И ИССЛЕДОВАНИЕ НА СХОДИМОСТЬ
Повторение: замечательные пределы
Для освоения материала нужно помнить пять замечательных пределов (в терминологии замены на эквивалентные):
1. 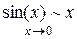


3. 

4. 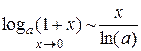

5. 

Вместо аргумента (икса) в замечательных пределах может также выступать функция, стремящаяся к нулю в искомой точке.
Например можно сказать, что 


Два типа несобственных интегралов
Несобственный интеграл первого типа имеет бесконечность в качестве одного или обоих пределов интегрирования б:

Несобственный интеграл второго типа похож на обычный определённый интеграл, но отличается от него тем, что значение подынтегральной функции 

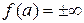
Пример несобственного интеграла первого типа:
Пример несобственного интеграла второго типа:
(он несобственный, т.к. значение подынтегральной функции в нуле бесконечно)
Как вычисляются несобственные интегралы?
Несобственные интегралы, которые существуют и имеют конечное значение, называются сходящимися, остальные – расходящимися. Вычисляются данные интегралы по уже знакомой нам теореме Ньютона-Лейбница, с той разницей, что мы не подставляем бесконечность в первообразную в буквальном смысле, а берём предел в ней.
Теорема Ньютона-Лейбница:
Примеры вычисления несобственных интегралов, которые являются сходящимися:
Если нам «не повезло», и в ответе получается бесконечное значение, то интеграл будет расходящимся. Пример:
Задачи для самостоятельного решения.
Вычислить или установить расходимость:
2.1 
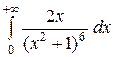
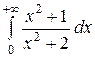
2.5
Исследование несобственных интегралов на сходимость.
Весьма часто возникает необходимость, не вычисляя значения самого несобственного интеграла, понять, сходится он или расходится. Для этого мы можем заменить его на другой, более простой, который не равен исходному, но сходится или расходится одновременно с исходным, т.е. в этом отношении «равносилен» ему. Для таких «расносильных» интегралов, в отличие от равенства, мы будем использовать значок 
Утверждение 1: если функции 





Утверждение 2: если функции 
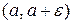


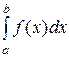
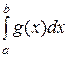
Аналогично, если если функции 
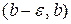


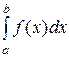
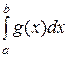
Итак, «равносильные» интегралы – это те, подынтегральные функции которых эквивалентны, и таким образом, сходящиеся или расходящиеся одновременно.
4. «Эталонные» интегралы (!)
В качестве «эталонных» интегралов, к которым мы будем сводить остальные, будут использоваться «интегралы с показателем p».
Для интегралов первого типа: 

Для интегралов второго типа: 

Данные утверждения легко проверить, непосредственно взяв первообразную от степенной функции под интегралом и подставив концы промежутка интегрирования.
Несобственные интегралы
Сначала рассмотрим интегралы с бесконечными пределами.
Определение 1.Пусть функция интегрируема на любом отрезке Тогда если существует конечный предел то говорят, что интеграл сходится. При этом пишут Если же указанный предел не существует или равен бесконечности, то говорят, что интеграл расходится.
Аналогично определяются интегралы
( здесь произвольная конечная точка). Эти интегралы называют несобственными интегралами первого рода. Их геометрический смысл ясен из рис. 11, где площадь Теперь рассмотрим интегралы от неограниченных функций.
Определение 2.Если функция не ограничена в окрестности точки (ее называют особой точкой ) и является интегрируемой на любом отрезке то по определению полагают Если этот предел существует и конечен, то говорят, что интеграл второго рода сходится. В противном случае он называется расходящимся. Аналогичный смысл имеют интегралы (второго рода)
где в первом случае точка является особой, а во втором случае точка является особой. Поскольку заменой переменной интеграл второго рода
( особая точка) сводится к интегралу первого рода, то будем изучать только интегралы с бесконечным верхним пределом. Сначала покажем, что эталонный интеграл
Переходя здесь к пределу при получаем наше утверждение. С помощью эталонного интеграла можно исследовать сходимость других несобственных интегралов.
Теорема сравнения 1.Пусть функции и интегрируемы на произвольном отрезке и имеют место неравенства Тогда если сходится интеграл то и сходится интеграл Если же интеграл расходится, то и расходится интеграл
Теорема сравнения 2. Пусть функции и положительны иинтегрируемы на произвольном отрезке Пусть, кроме того, существует предел Тогда интегралы и сходятся или расходятся одновременно.
Замечание 1. При примененииэтих теорем часто используется таблица эквивалентных бесконечно малых:
Если при то при верны следующие соотношения:
Например, интеграл сходится, так как и интеграл сходится (см. эталонный интеграл( ) и теорему сравнения 2).
Отметим, что теоремы сравнения верны лишь для неотрицательных подынтегральных функций. Если эти функции не являются знакопостоянными, то вводят понятие абсолютной сходимости: говорят, что интеграл сходится абсолютно, если сходится интеграл Если последний интеграл расходится, а сам интеграл сходится, то его называют условно сходящимся интегралом. Нетрудно показать, что из сходимости интеграла вытекает обычная сходимость интеграла Обратное, вообще говоря, неверно. Можно показать, например, что интеграл
сходится, а интеграл расходится. Тем не менее, при исследовании сходимости интегралов от знакопеременных функций изучают сначала их абсолютную сходимость (здесь можно применить теоремы сравнения), а затем – условную сходимость.
Так как интеграл сходится, то и интеграл также сходится, а, значит, исходный интеграл сходится абсолютно.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Несобственные интегралы



Сначала рассмотрим интегралы с бесконечными пределами.
Определение 1.Пусть функция интегрируема на любом отрезке Тогда если существует конечный предел то говорят, что интеграл сходится. При этом пишут Если же указанный предел не существует или равен бесконечности, то говорят, что интеграл расходится.
Аналогично определяются интегралы
( здесь произвольная конечная точка). Эти интегралы называют несобственными интегралами первого рода. Их геометрический смысл ясен из рис. 11, где площадь Теперь рассмотрим интегралы от неограниченных функций.
Определение 2.Если функция не ограничена в окрестности точки (ее называют особой точкой ) и является интегрируемой на любом отрезке то по определению полагают Если этот предел существует и конечен, то говорят, что интеграл второго рода сходится. В противном случае он называется расходящимся. Аналогичный смысл имеют интегралы (второго рода)
где в первом случае точка является особой, а во втором случае точка является особой. Поскольку заменой переменной интеграл второго рода
( особая точка) сводится к интегралу первого рода, то будем изучать только интегралы с бесконечным верхним пределом. Сначала покажем, что эталонный интеграл
Переходя здесь к пределу при получаем наше утверждение. С помощью эталонного интеграла можно исследовать сходимость других несобственных интегралов.
Теорема сравнения 1.Пусть функции и интегрируемы на произвольном отрезке и имеют место неравенства Тогда если сходится интеграл то и сходится интеграл Если же интеграл расходится, то и расходится интеграл
Теорема сравнения 2. Пусть функции и положительны иинтегрируемы на произвольном отрезке Пусть, кроме того, существует предел Тогда интегралы и сходятся или расходятся одновременно.
Замечание 1. При примененииэтих теорем часто используется таблица эквивалентных бесконечно малых:
Если при то при верны следующие соотношения:
Например, интеграл сходится, так как и интеграл сходится (см. эталонный интеграл( ) и теорему сравнения 2).
Отметим, что теоремы сравнения верны лишь для неотрицательных подынтегральных функций. Если эти функции не являются знакопостоянными, то вводят понятие абсолютной сходимости: говорят, что интеграл сходится абсолютно, если сходится интеграл Если последний интеграл расходится, а сам интеграл сходится, то его называют условно сходящимся интегралом. Нетрудно показать, что из сходимости интеграла вытекает обычная сходимость интеграла Обратное, вообще говоря, неверно. Можно показать, например, что интеграл
сходится, а интеграл расходится. Тем не менее, при исследовании сходимости интегралов от знакопеременных функций изучают сначала их абсолютную сходимость (здесь можно применить теоремы сравнения), а затем – условную сходимость.
Так как интеграл сходится, то и интеграл также сходится, а, значит, исходный интеграл сходится абсолютно.
Сегодня вы поймёте, что такое интеграл в математике
(и в программировании)
Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали.
Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него.
Но сначала: что такое функция
Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них.
Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием.
У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число.
Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел.
Что такое интеграл
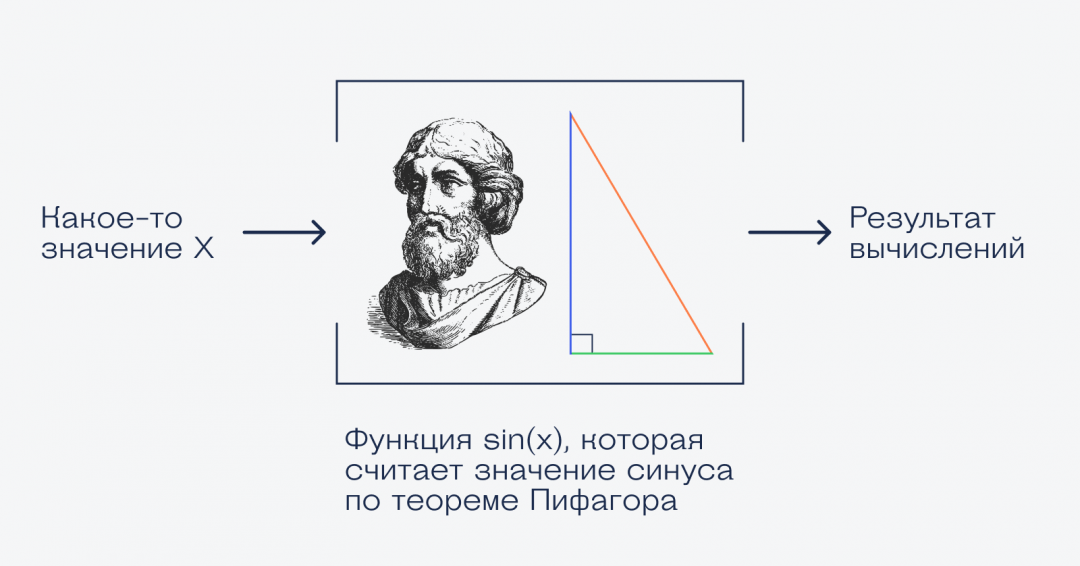
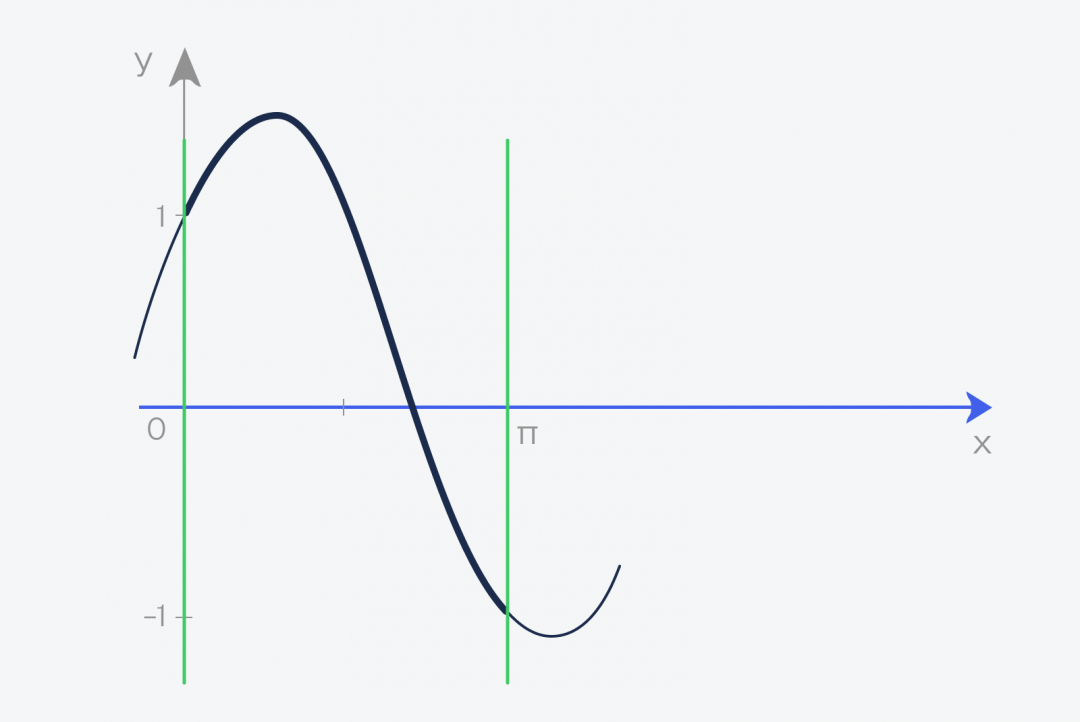
Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции.
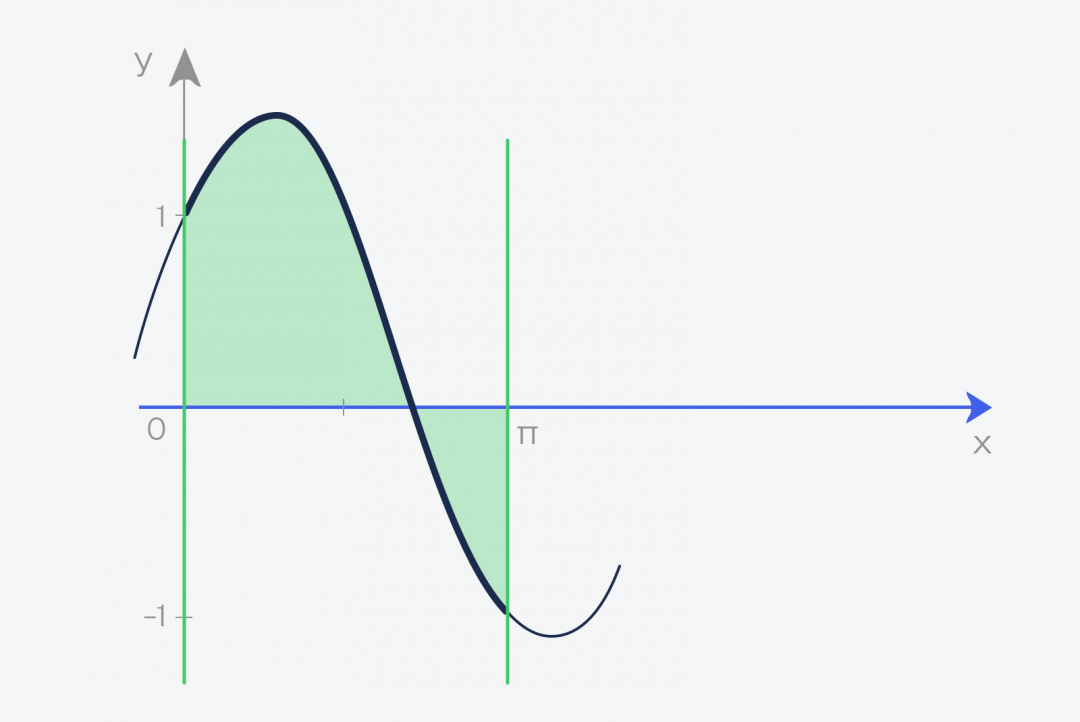
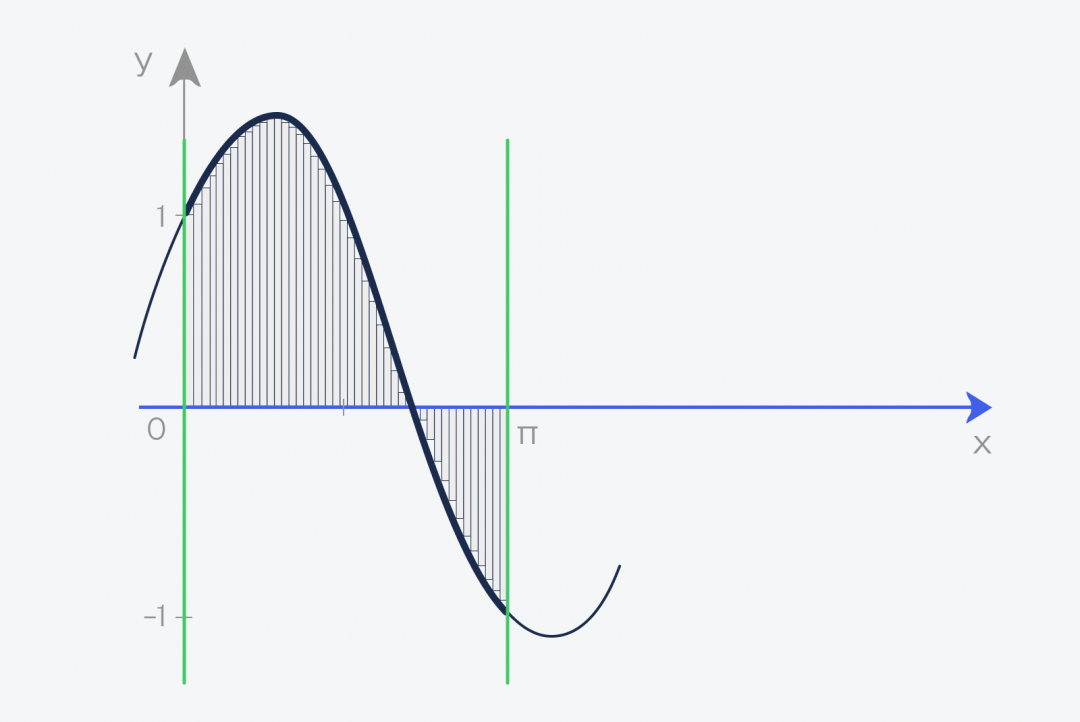
Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:
А теперь то, ради чего всё это затевалось:
✅ Площадь этой фигуры и есть интеграл функции f(x) = sin(x) + cos(x) на отрезке от a до b
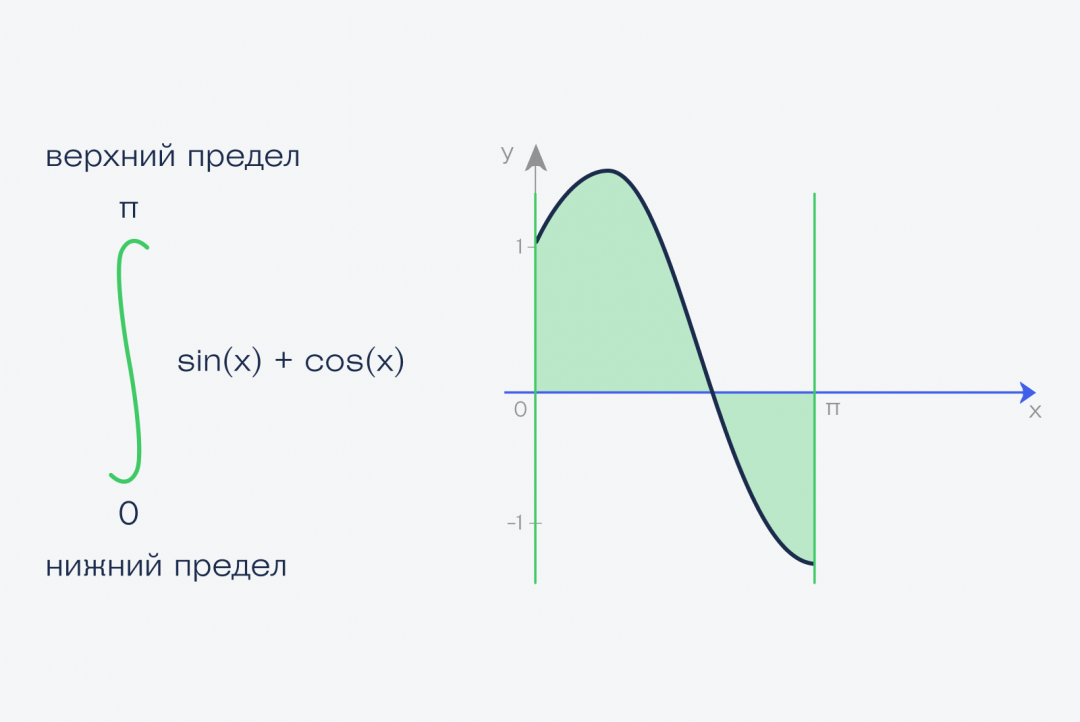
В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926.
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:
В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.
Зачем нужны интегралы в народном хозяйстве
Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона.
Интегралы нужны в математике и физике, это один из инструментов вычислений.
Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца.
Как посчитать интеграл (то есть найти площадь)
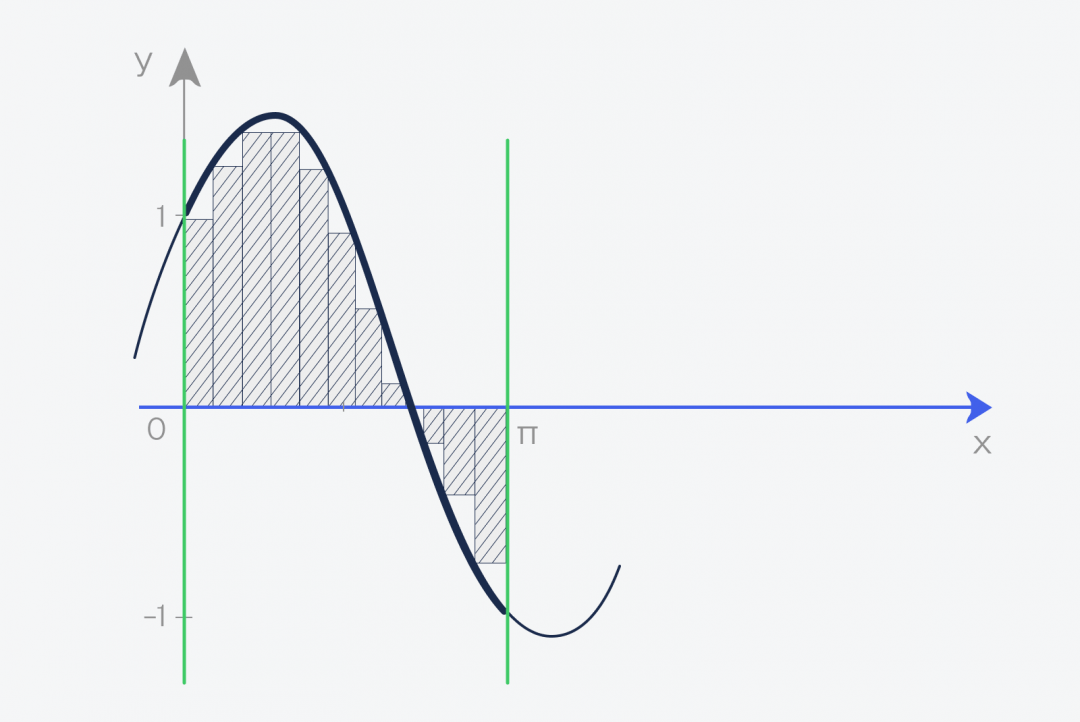
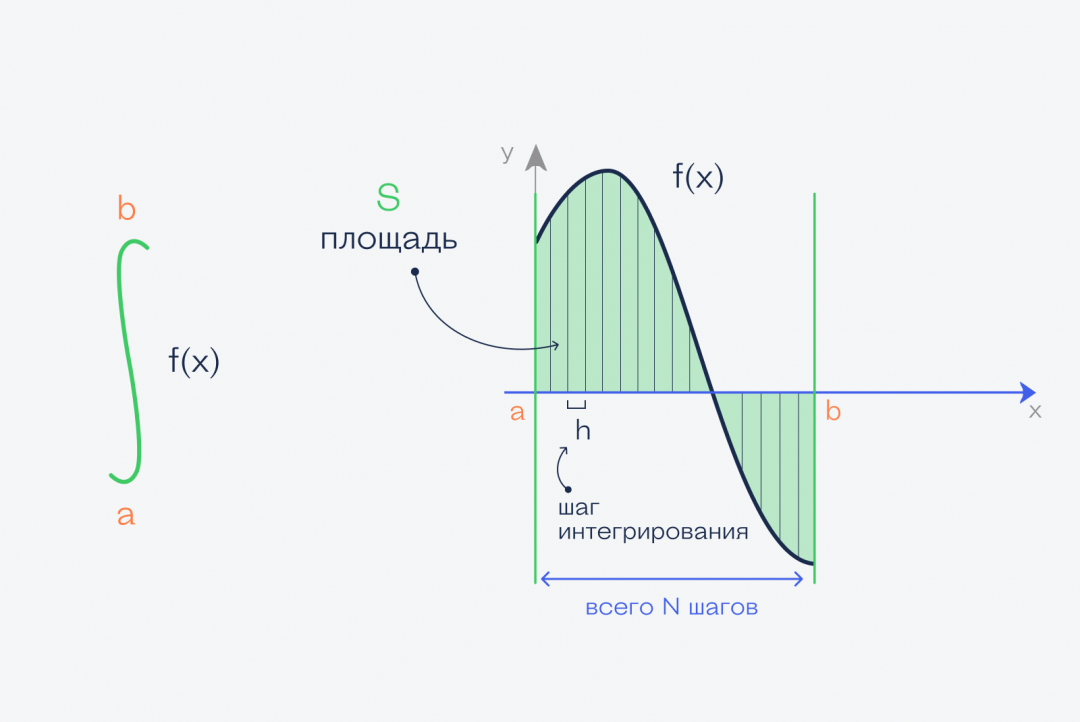
Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.
Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.
Пишем код
Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.
Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).
Общая логика работы будет такая:
На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:
Что дальше
Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно.
В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.