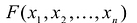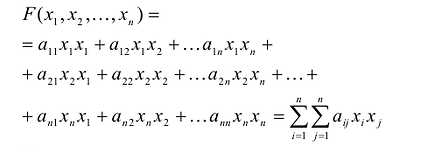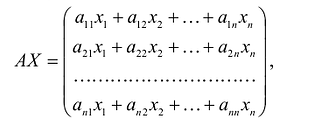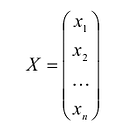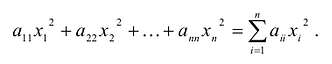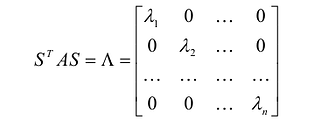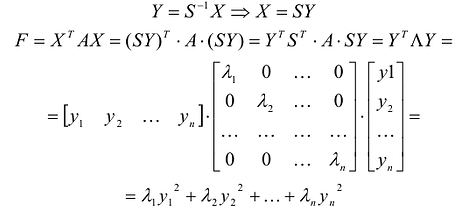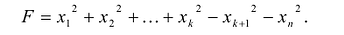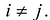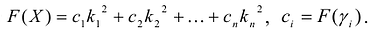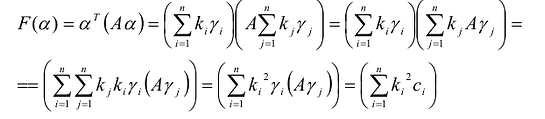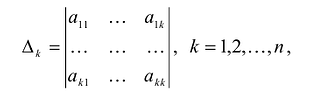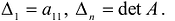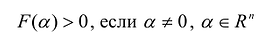диагональный вид квадратичной формы

Приведение квадратичной формы к диагональному виду методом элементарных преобразований.

Приведение квадратичной формы к диагональному виду методом Лагранжа.

Канонический вид квадратичной формы. Положительный и отрицательный индексы инерции квадратичной формы. Ранг квадратичной формы.

Квадратичная форма называется канонической, если все т. е.

Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

1. Ортогональное преобразование пространства :

где — собственные значения матрицы A.

Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем

3. Метод Якоби (в случае, когда все главные миноры квадратичной формы отличны от нуля):

Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.

В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.

В этом базисе квадратичная форма имеет канонический вид

Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.

Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность междуположительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.

Положительно определенные квадратичной формы. Критерий Сильвестра.

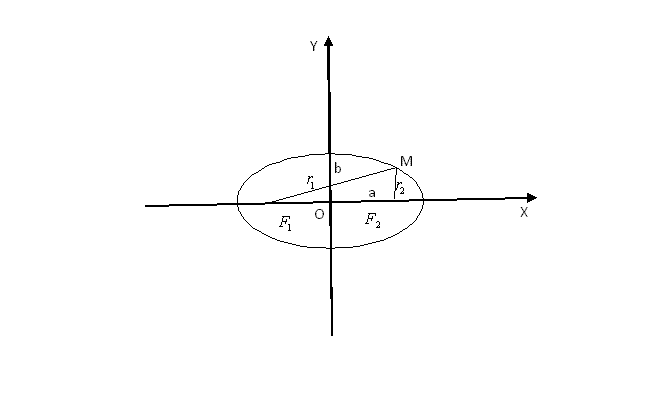
Определение эллипса. Фокусы эллипса.

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.

Теорема. Фокусное расстояние и полуоси связаны соотношением:

Дата добавления: 2018-05-12 ; просмотров: 2004 ; Мы поможем в написании вашей работы!

Источник

§3. Приведение квадратичной формы к диагональному и каноническому виду

называется диагональным видом квадратичной формы. Говорим, что квадратичная форма k(x) приведена к диагональному виду, если указан такой базис, в котором она имеет вид (6.4). Если в (6.4) все коэффициенты ₁, ₂,…, _n равны 1, 1 или 0, то говорим, что k(x) имеет канонический вид.

Теорема 6.2. Всякую квадратичную форму, определённую на векторном пространстве L n , с помощью выбора нового базиса можно привести к диагональному виду. Причём, если пространство является евклидовым, мы можем это сделать с помощью выбора нового ОНБ.

Доказательство. Пусть сначала наше пространство является евклидовым. Пусть k(x) – квадратичная форма, f(x,y) – полярная ей билинейная функция, A – соответствующий ей самосопряженный оператор. Выберем такой ОНБ, в котором матрица оператора имеет диагональный вид:

Тогда k(x) тоже будет иметь такую же матрицу, а значит, будет иметь вид (6.4). Напомним, что базис, в котором матрица оператора имеет вид (6.5), состоит из собственных векторов оператора, а ₁, ₂,…, _n – это его собственные числа.

Впроизвольном векторном пространстве мы можем ввести скалярное произведение и, тем самым, превратить его в евклидово пространство. Для этого достаточно произвольный базис объявить ортонормированным. Тогда мы сможем применить описанный выше метод приведения к диагональному виду.

Существует и другой метод приведения квадратичной формы к диагональному виду в произвольном векторном пространстве, который мы рассмотрим на примере. Это метод выделения полных квадратов. Пусть в пространстве L 3

Теперь мы группируем вместе все слагаемые, содержащие x 2 и дополняем это выражение до полного квадрата; добавленное вычитаем.

Делаем теперь замену координат:

Теперь мы можем выписать матрицу перехода

а по ней выписываем формулы замены базиса:

Подчеркнём, что данная процедура используется только в том случае, когда не ставится задача найти новый ОНБ в евклидовом пространстве.

Теорема 6.3. Всякую квадратичную форму, определённую на векторном пространстве L n , с помощью выбора нового базиса можно привести к каноническому виду.

Базис, в котором квадратичная форма имеет диагональный вид, может не быть единственным. Если мы приводим квадратичную форму к диагональному виду в евклидовом пространстве с помощью ортогонального преобразования, то коэффициенты ₁, ₂,…, _n – это собственные числа соответствующего линейного оператора. Значит эти коэффициенты не зависят от того, какой именно ОНБ мы выбираем. Применительно к произвольным заменам базиса действует следующая теорема.

Теорема 6.4. (Закон инерции квадратичной формы) Число отрицательных, число положительных и число нулевых коэффициентов _i в каноническом или диагональном виде квадратичной формы не зависит от выбора базиса, в котором квадратичная форма приведена к этому виду (без доказательства).

Определение. Говорим, что квадратичная форма имеет сигнатуру

(k, l, m) или (+,…,+,,…,,0,…,0),

если в её диагональном виде есть k положительных коэффициентов, l отрицательных и m нулевых.

Определение. Назовём главными минорами матрицы её левые верхние угловые миноры, т.е. миноры вида

Теорема 6.5. (Критерий Сильвестра) Квадратичная форма положительно определена тогда и только тогда, когда все её главные угловые миноры положительны. Квадратичная форма отрицательно определена тогда и только тогда, когда её главные угловые миноры чередую знаки и a₁₁ 22 / 25 22 23 24 25 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

риведение квадратичной формы к диагональному виду.

Определение. Пусть в евклидовом пространстве V 3 задана декартова система координат (x, y, z), k( ) – квадратичная форма, имеющая вид (12), A – её матрица.

Если в пространстве ввести другую систему координат, то тем же точкам будут соответствовать другие координаты, а значение функции в этих точках должно остаться прежним. Поэтому выражение (12) должно иметь другой вид. Пусть C – матрица перехода к новой системе координат (x¢, y¢, z¢), а A¢ – матрица квадратичной формы k( ) относительно новой системы. Тогда матрицы A и A¢ связаны между собой формулой

A¢= C Т AC. (11)

В задачах на приведение квадратичной формы к каноническому виду обязательно нужно выписать формулы перехода от старых координат (x, y, z) к новым координатам (x¢, y¢, z¢):

или формулы перехода от новых координат к старым:

где C – матрица перехода, а X и X¢ – координатные столбцы:

то матрица C составляется следующим образом:

Тогда в развернутом виде формулы (14¢) имеют вид:

x = c₁ 1 x¢ + c₂ 1 y¢ + c₃ 1 z¢,

x¢= c₁ 1 x + c₁ 2 y + c₁ 3 z,

Для решения задач, связанных с приведением уравнения поверхности второго порядка к каноническому виду, нам понадобятся именно формулы (14¢), выражающие старые координаты через новые.

Пример 3.В пространстве V 3 квадратичная форма k() определяется относительно декартовой системы координат (x, y, z) формулой

С помощью выбора новой системы координат (x¢, y¢, z¢) привести k() к диагональному виду.

Мы видим, что матрица A совпадает с матрицей из примера 2, находим собственные числа и соответствующие им собственные векторы

Новые координаты выражаются через старые по формулам:

x¢= x + z,

Старые координаты выражаются через новые по формулам:

x = x¢ + y¢ + z¢,

Источник

Диагональный вид квадратичной формы

Приведение квадратичной формы к каноническому виду методом Лагранжа.

При приведении квадратичной формы к диагональному виду (каноническому виду) можно воспользоваться методом выделения квадратов (методом Лагранжа). Покажем его на примере. Пусть задана квадратичная форма

k ( x )=

Заметив, что коэффициент при отличен от нуля, соберем вместе все члены, содержащие :

Дополним выражение в квадратных скобках до квадрата суммы, прибавив и вычтя :

k ‘( x ) =

К ней можно применить тот же прием:

k ‘( x ) =

k ( x ) =

Последние формулы задают преобразование координат при переходе к базису, в котором квадратичная форма имеет диагональный вид.

Теорема инерции для квадратичных форм.

Теорема. Число отрицательных и число положительных коэффициентов в каноническом виде квадратичной формы не зависят от базиса, в котором она приведена к каноническому виду.

Обозначим через линейную оболочку векторов , а через — линейную оболочку остальных базисных векторов. Для любого имеем , и

k(x)= , если только . Значит, k отрицательно определена на и .

На форма k положительно полуопределенная, потому что для любого и (Форма может равняться нулю только на ненулевом веткторе, если )

Следствие. Число положительных и число отрицательных коэффициентов в любом диагональном виде квадратичной формы не зависят от базиса.

Знакоопределенные квадратичные формы.

Определение. Квадратичную форму k будем называть положительно определенной на пространстве пространства , если для любого ненулевого вектора x из . Форма k отрицательно определена на , если для любого из .

Если говорят, что квадратичная форма положительно или отрицательно определена, без уточнения подпространства, то она обладает таким свойством на всем .

Квадратичные формы, для которых или при любом x , называются соответственно положительно или отрицательно полуопределенными.

Удобно считать, что на нулевом подпространстве каждая квадратичная форма положительно определена, и отрицательно определена одновременно. В силу этого соглашения всегда существует (хотя бы нулевое) подпространство, на котором квадратичная форма отрицательно определена.

Теорема. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы миноры ее матрицы удовлетворяли неравенствам

>0 ( k =1. n ) (13)

Миноры вида (13) называются главными минорами матрицы.

Для доказательства вспомним преобразования матрицы квадратичной формы.

1. Необходимость. Если квадратичная форма k положительно определена, то диагональные элементы ее матрицы в любом базисе удовлетворяют условию

и, следовательно, при приведении матрицы к диагональному виду особый случай не встретится. В основном случае к любой строке может быть прибавлена только лежащая выше, а к любому столбцу – только расположенный левее. При таких преобразованиях главные миноры матрицы не меняются. Но у диагональной матрицы для положительно определенной квадратичной формы главные миноры положительны. Потому они положительны и у исходной матрицы.

2. Достаточность. Пусть все главные миноры матрицы B положительны. В частности,

, и первый шаг преобразования приводит матрицу к виду

с . Допустим, что после k шагов мы получили матрицу с положительными причем не возникало особого случая. Тогда для левого верхнего элемента матрицы имеем

Источник

Содержание:

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Понятие квадратичной формы

Квадратичной формой

Пример:

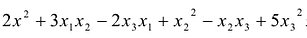
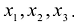
Сумма является квадратичной формой от трех неизвестных .

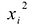
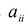
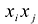
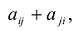
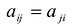
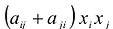
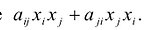
Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при обозначаются через а коэффициенты при через причем „ Член записывается в виде После этих преобразований квадратичную форму можно записать в виде:

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

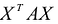
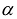
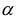
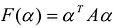
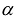
результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид . Если — произвольный n— мерный вектор, то после подстановки в квадратичную форму вместо X получится число , которое называется значением квадратичной формы F(X) на векторе .

Канонический базис квадратичной формы

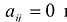
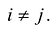
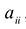
Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. при . При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами ,т.е.:

В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

где 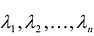-собственные значения матрицы А.

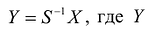
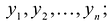
Применим к квадратичной форме линейное преобразование — матрица-столбец новых переменных — матрица, обратная к S.

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

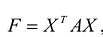
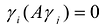
Базис пространства R» называется каноническим базисом квадратичной формы , если в этом базисе квадратичная форма имеет канонический вид, т.е. при

Если канонический базис F(X), то выражение: называется каноническим видом F(X) в базисе где — новый набор неизвестных.

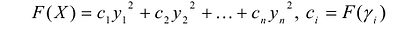
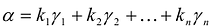
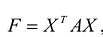
Теорема. Если — разложение вектора а по каноническому базису квадратичной формы то значение F(X) на векторе а вычисляется по формуле

Доказательство:

Эта теорема утверждает, что если известны канонический базис квадратичной формы F(X) и ее канонический вид в этом базисе, то для вычисления значения F(a) квадратичной формы F(X) на векторе а достаточно:

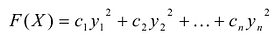
Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов симметрической матрицы , является каноническим базисом квадратичной формы , а выражение — ее каноническим видом в базисе ,

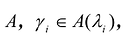
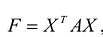
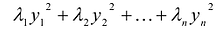
Доказательство:

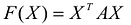
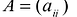
Канонический базис Якоби квадратичной формы . Будем говорить, что матрица удовлетворяет условию Якоби, если определители:

называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что

Обозначим через 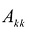матрицу:

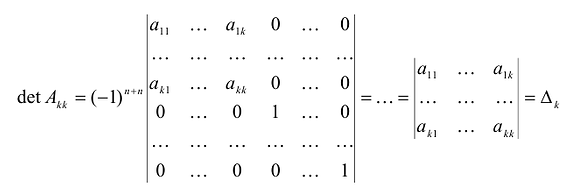
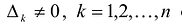
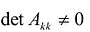
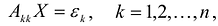
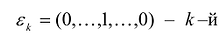
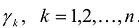
Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. Из условия следует, что и, значит, каждая система уравнений , где вектор диагональной системы, имеет единственное решение . Система векторов называется системой векторов Якоби матрицы А, которая удовлетворяет условию Якоби.

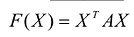
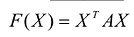
Теорема. матрица А квадратичной формы удовлетворяет условию Якоби, система векторов Якоби матрицы А является каноническим базисом квадратичной формы , а выражение:

ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник