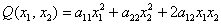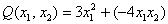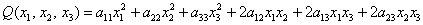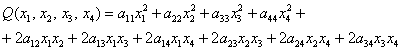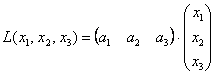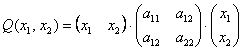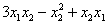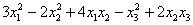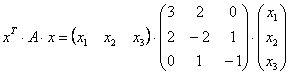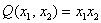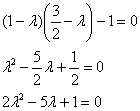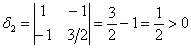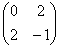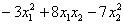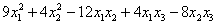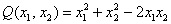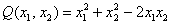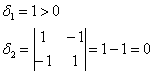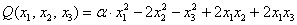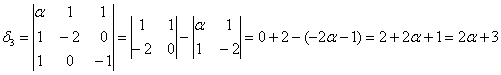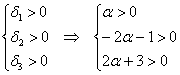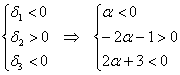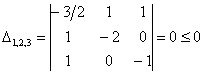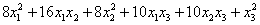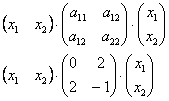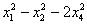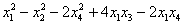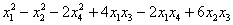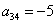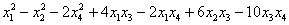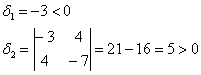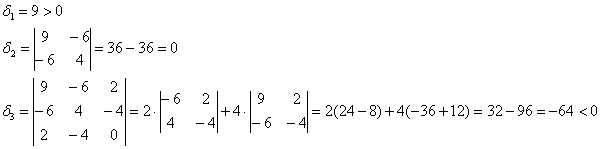как привести квадратичную форму к диагональному виду
Приведение квадратичной формы к диагональному виду методом элементарных преобразований.
Приведение квадратичной формы к диагональному виду методом Лагранжа.
Канонический вид квадратичной формы. Положительный и отрицательный индексы инерции квадратичной формы. Ранг квадратичной формы.
Квадратичная форма называется канонической, если все 
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1. Ортогональное преобразование пространства 
где 
Затем подобную процедуру проделывают с квадратичной формой 




3. Метод Якоби (в случае, когда все главные миноры 
Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.
Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность междуположительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
Положительно определенные квадратичной формы. Критерий Сильвестра.
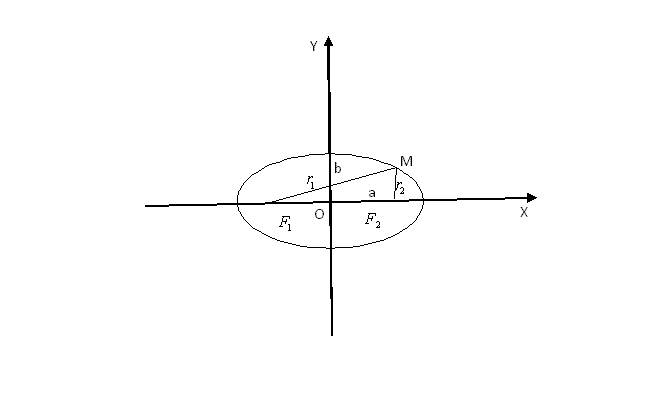
Определение эллипса. Фокусы эллипса.
с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.
Теорема. Фокусное расстояние и полуоси связаны соотношением:
Дата добавления: 2018-05-12 ; просмотров: 2030 ; Мы поможем в написании вашей работы!
§3. Приведение квадратичной формы к диагональному и каноническому виду
называется диагональным видом квадратичной формы. Говорим, что квадратичная форма k(x) приведена к диагональному виду, если указан такой базис, в котором она имеет вид (6.4). Если в (6.4) все коэффициенты 1, 2,…, n равны 1, 1 или 0, то говорим, что k(x) имеет канонический вид.
Теорема 6.2. Всякую квадратичную форму, определённую на векторном пространстве L n , с помощью выбора нового базиса можно привести к диагональному виду. Причём, если пространство является евклидовым, мы можем это сделать с помощью выбора нового ОНБ.
Доказательство. Пусть сначала наше пространство является евклидовым. Пусть k(x) – квадратичная форма, f(x,y) – полярная ей билинейная функция, A – соответствующий ей самосопряженный оператор. Выберем такой ОНБ, в котором матрица оператора имеет диагональный вид:
Тогда k(x) тоже будет иметь такую же матрицу, а значит, будет иметь вид (6.4). Напомним, что базис, в котором матрица оператора имеет вид (6.5), состоит из собственных векторов оператора, а 1, 2,…, n – это его собственные числа.
В
Существует и другой метод приведения квадратичной формы к диагональному виду в произвольном векторном пространстве, который мы рассмотрим на примере. Это метод выделения полных квадратов. Пусть в пространстве L 3
Теперь мы группируем вместе все слагаемые, содержащие x 2 и дополняем это выражение до полного квадрата; добавленное вычитаем.
Делаем теперь замену координат:
Теперь мы можем выписать матрицу перехода
а по ней выписываем формулы замены базиса:
Подчеркнём, что данная процедура используется только в том случае, когда не ставится задача найти новый ОНБ в евклидовом пространстве.
Теорема 6.3. Всякую квадратичную форму, определённую на векторном пространстве L n , с помощью выбора нового базиса можно привести к каноническому виду.
Базис, в котором квадратичная форма имеет диагональный вид, может не быть единственным. Если мы приводим квадратичную форму к диагональному виду в евклидовом пространстве с помощью ортогонального преобразования, то коэффициенты 1, 2,…, n – это собственные числа соответствующего линейного оператора. Значит эти коэффициенты не зависят от того, какой именно ОНБ мы выбираем. Применительно к произвольным заменам базиса действует следующая теорема.
Теорема 6.4. (Закон инерции квадратичной формы) Число отрицательных, число положительных и число нулевых коэффициентов i в каноническом или диагональном виде квадратичной формы не зависит от выбора базиса, в котором квадратичная форма приведена к этому виду (без доказательства).
Определение. Говорим, что квадратичная форма имеет сигнатуру
(
если в её диагональном виде есть k положительных коэффициентов, l отрицательных и m нулевых.
Определение. Назовём главными минорами матрицы её левые верхние угловые миноры, т.е. миноры вида
Теорема 6.5. (Критерий Сильвестра) Квадратичная форма положительно определена тогда и только тогда, когда все её главные угловые миноры положительны. Квадратичная форма отрицательно определена тогда и только тогда, когда её главные угловые миноры чередую знаки и a11 22 / 25 22 23 24 25 > Следующая > >>
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра
Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась 🙂
Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную. Линейной формой 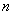
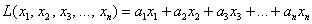
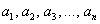
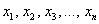
* В рамках данной темы будем рассматривать только действительные числа.
С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений, и в данном случае он подразумевает, что у многочлена нет приплюсованной константы 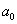
Например: 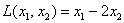
Теперь форма квадратичная. Квадратичной формой 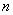
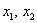
Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
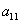
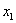
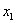
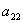
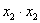
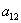
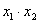
Далее будем полагать, что хотя бы одна из констант не равна нулю, и вот, пожалуйста, «неполный» пример: 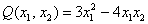
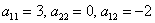
Иногда встречается «школьный» вариант оформления в духе 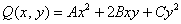
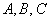
И квадратичная форма трёх переменных содержит уже шесть членов:
…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.
Далее ситуация начинает усугубляться:
и усугублять мы её дальше не будем, т.к. формы с бОльшим количеством переменных встречаются довольно редко.
Однако общую формулу запишем, её удобно оформить «простынёй»:
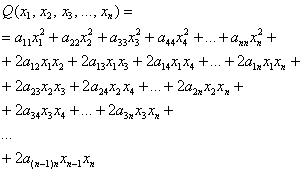
– внимательно изучаем каждую строчку – ничего страшного тут нет!
Квадратичная форма содержит 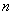
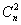
Матричная запись квадратичной формы
Как на счёт матриц? 🙂 Знаю, знаю, соскучились. В практических задачах широко распространенная матричная запись квадратичных форм. Объяснения опять начну с формы линейной, например, от трёх переменных: 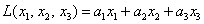
И действительно, выполняя матричное умножение, получаем матрицу «один на один»: 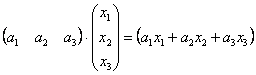
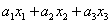
Легко понять, что линейная форма «эн» переменных записывается в виде:
Квадратичная форма представима в виде произведения уже трёх матриц:
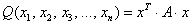
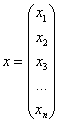
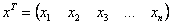

Это так называемая симметрическая матрица, на главной диагонали которой расположены коэффициенты 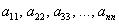
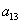
Определитель 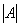
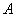
Если перемножить три матрицы 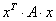
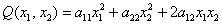
И в самом деле: 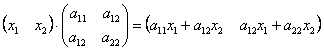
далее: 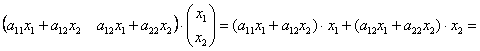
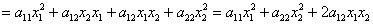
Как вариант, сначала можно было перемножить правые матрицы, и затем первую матрицу умножить на полученный результат.
Вам понравилось так же, как и мне? Ну тогда пример для самостоятельного решения =)
Записать квадратичную форму в матричном виде и выполнить проверку. Определить дискриминант и ранг формы.
…что-то смущает? 😉 Краткое решение и ответ в конце урока! Статьи об определителе и ранге матрицы – в помощь.
После чего разберём аналогичную задачу с формой трёх переменных:
Записать матрицу квадратичной формы, найти её ранг и дискриминант
Решение: сбросим тяжёлую ношу лишних формул, и будем ориентироваться на сами члены:
– слагаемое 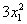
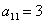
– из аналогичных соображений определяем 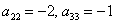
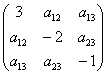
Так как в слагаемое 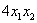
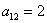
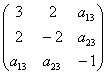
Поскольку в форме отсутствует член с произведением 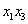
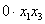
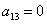
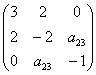
И, наконец, из слагаемого 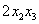
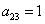
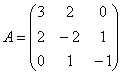
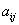
По условию не требовалось записывать матричное уравнение, однако науки ради:
Желающие могут перемножить три матрицы, в результате чего должна получиться исходная квадратичная форма.
Теперь определим ранг формы. Он равен рангу матрицы 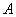
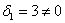
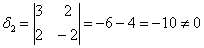
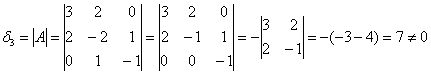
Если не очень понятно, что к чему, обязательно изучите статью о ранге матрицы – это довольно замысловатая задачка, и перед нами оказался лишь простой случай, когда угловые миноры не равны нулю.
Дискриминант квадратичной формы получен автоматом.
Ответ: 
Следующее задание для самостоятельного решения:
Восстановить квадратичную форму по её матрице
При этом не нужно вспоминать никаких формул! Решение почти устное:
– сначала смотрим на главную диагональ и записываем слагаемые с квадратами переменных;
– затем анализируем симметричные элементы 1-й строки (или 1-го столбца), и записываем все слагаемые, в которые входит 1-я переменная (не забывая удвоить коэффициенты);
– далее смотрим на оставшиеся симметричные элементы 2-й строки (справа от диагонали) либо 2-го столбца (ниже диагонали) и записываем соответствующие парные произведения (с удвоенными коэффициентами!).
– и, наконец, анализируем правую нижнюю пару симметричных чисел.
Подробное решение и ответ в конце урока.
Знакоопределённость квадратичной формы. Критерий Сильвестра
До сих пор мы рассматривали «внешнее устройство» форм и пришло время изучить их функциональное назначение. Да, по существу, они работают, как функции. Вернёмся к простенькой линейной форме 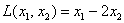
Как отмечалось в начале урока, переменные 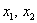
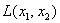
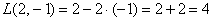
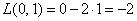
Говоря языком науки, перед нами скалярная функция векторного аргумента, в которой каждому вектору 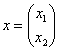
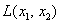
В зависимости от значений 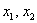
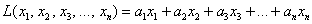
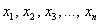
Такая форма называется знакопеременной. И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:
Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной.
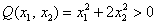
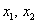
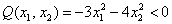
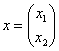
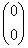
И вообще, если для любого ненулевого вектора 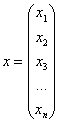
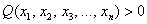
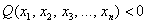
Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения 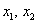
На этот счёт существует теорема: если ВСЕ собственные числа матрицы квадратичной формы положительны*, то она определена положительно. Если все отрицательны – то отрицательно.
* В теории доказано, что все собственные числа действительной симметрической матрицы действительны
Запишем матрицу вышеприведённой формы:
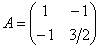
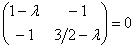
Решаем старое доброе квадратное уравнение: 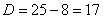
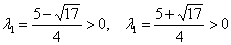
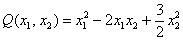
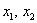
Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.
Как быть? Существует более простой путь!
Критерий Сильвестра
Нет, не Сильвестра Сталлоне 🙂 Сначала напомню, что такое угловые миноры матрицы. Это определители 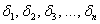

и последний из них в точности равен определителю матрицы.
Теперь, собственно, критерий:
1) Квадратичная форма определена положительно тогда и только тогда, когда ВСЕ её угловые миноры больше нуля: 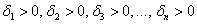
2) Квадратичная форма определена отрицательно тогда и только тогда, когда её угловые миноры знакочередуются, при этом 1-й минор меньше нуля: 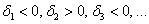
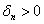
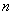
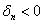
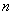
Если в 1-й или 2-й последовательности есть нулевые миноры, то это два особых случая, которые я разберу чуть позже, после того, как мы перещёлкаем более распространённые примеры. При любой другой комбинации плюсов-минусов (и опционально нулей) форма знакопеременна.
Проанализируем угловые миноры матрицы 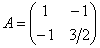
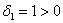
Вывод: все угловые миноры больше нуля, значит, форма 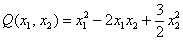
Есть разница с методом собственных чисел? 😉
Запишем матрицу формы 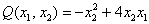
первый её угловой минор 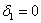
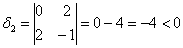
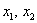
Возьмём форму 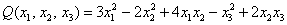
тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём: 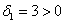
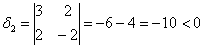
Вывод: форма знакопеременна.
Разминочные примеры для самостоятельного решения:
Исследовать квадратичные формы на знакоопределенность
а)
б)
В этих примерах всё гладко (см. конец урока), но на самом деле для выполнения такого задания критерия Сильвестра может оказаться не достаточно.
Дело в том, что существуют «краевые» случаи, а именно: если для любого ненулевого вектора 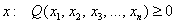
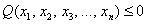
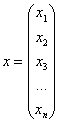
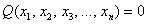
Здесь можно привести такой «баян»:
Выделяя полный квадрат, сразу видим неотрицательность формы: 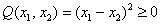
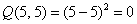
«Зеркальный» пример неположительно определённой формы: 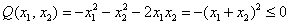
и ещё более тривиальный пример:
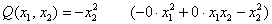
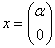
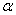
Как выявить неотрицательность или неположительнось формы?
Для этого нам потребуется понятие главных миноров матрицы. Главный минор – это минор, составленный из элементов, которые стоят на пересечении строк и столбцов с одинаковыми номерами. Так, у матрицы 
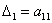
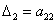
и один главный минор 2-го порядка:
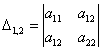
У матрицы «три на три» 
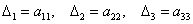
три минора 2-го порядка:
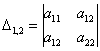
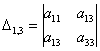
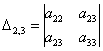
и один минор 3-го порядка:
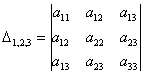
Задание на понимание: записать все главные миноры матрицы 
Сверяемся в конце урока и продолжаем.
Критерий Шварценеггера:
1) Ненулевая* квадратичная форма определена неотрицательно тогда и только тогда, когда ВСЕ её главные миноры неотрицательны (больше либо равны нулю).
* У нулевой (вырожденной) квадратичной формы все коэффициенты равны нулю.
2) Ненулевая квадратичная форма с матрицей 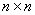
– главные миноры 1-го порядка неположительны (меньше либо равны нулю);
– главные миноры 2-го порядка неотрицательны;
– главные миноры 3-го порядка неположительны (пошлО чередование);
…
– главный минор 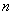
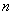
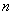
Если хотя бы один минор противоположного знака, то форма знакопеременна.
Посмотрим, как работает критерий в вышеприведённых примерах:
Составим матрицу 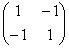
Полученные значения не удовлетворяют критерию Сильвестра, однако второй минор не отрицателен, и это вызывает надобность проверить 2-й критерий (в случае 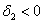
Главные миноры 1-го порядка:
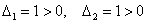
главный минор 2-го порядка:
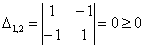
Таким образом, ВСЕ главные миноры не отрицательны, значит, форма неотрицательна.
Запишем матрицу 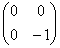
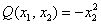
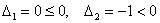
главный минор 2-го порядка:
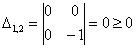
Таким образом, по критерию Шварценеггера (пункт 2), форма определена неположительно.
Теперь во всеоружии разберём более занятную задачку:
Исследовать квадратичную форму на знакоопределенность
Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.
Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:
Вычислим угловые миноры: 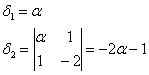
третий определитель я раскрою по 3-й строке:
Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.
Дальнейшее решение удобно разбить на 2 пункта:
1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:
В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством: 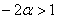
умножим обе его части на 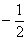
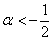
Таким образом, система несовместна, а значит, форма не может быть положительно определённой ни при каких «альфа», из чего логически и автоматически следует, что она не может быть и неотрицательной.
2) Проведём исследование на отрицательность / неположительнось. По Сильвестру, условию отрицательности формы соответствует следующая система линейных неравенств:
Второе неравенство уже решено: 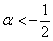
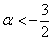
Таким образом, имеем совместную систему: 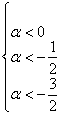
из которой следует, что форма определена отрицательно при 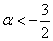
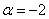
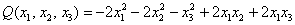
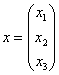
Осталось исследовать «пограничный» случай. Если 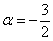
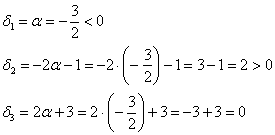
Последнее значение не удовлетворяет 2-му пункту критерия Сильвестра, однако оно равно нулю, что позволяет предположить неположительнось формы. Запишем матрицу 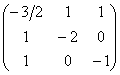
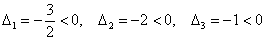
Рассчитываем миноры 2-го порядка. Если хотя бы один из них окажется отрицательным, то форма будет знакопеременной:
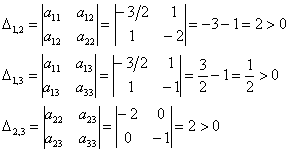
Нет, все миноры неотрицательны, и минор 3-го порядка уже рассчитан:
Таким образом, по критерию Шварценеггера (пункт 2), имеет место неположительнось формы, иными словами, 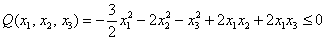
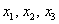
Ответ: при 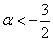
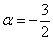
И творческое задание для самостоятельного решения:
Исследовать квадратичную форму на знакоопределенность
И в заключение статьи хочу выразить благодарность Сергею Хохлову, некогда ст. преподавателю МПГУ – за важные замечания и интересные дополнительные примеры, а также Арнольду Шварценеггеру, который сыграл в непривычном для себя амплуа и помог мне ярче объяснить материал 🙂
Как сказал актёр, I’ll be back, и я жду вас на следующем уроке – о каноническом виде квадратичной формы.
Пример 1. Решение: сначала приведём подобные слагаемые: 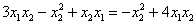
Квадратичная форма двух переменных имеет вид 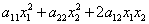
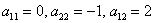
Проверка: 
что и требовалось проверить.
Вычислим дискриминант формы: 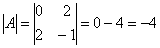
Поскольку 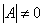
Ответ: 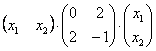
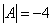
Пример 3. Решение: симметрическая матрица 4*4 определяет квадратичную форму 4 переменных. Коэффициенты главной диагонали 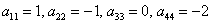
Симметричные коэффициенты 1-й строки: 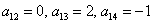
Оставшиеся симметричные элементы 2-й строки: 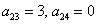
И, наконец,
Ответ:
Пример 4. Решение:
а) запишем матрицу формы: 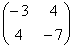
и вычислим её угловые миноры:
Таким образом, по критерию Сильвестра, форма определена отрицательно.
б) запишем матрицу формы: 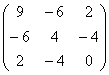
и вычислим её угловые миноры:
Вывод: форма знакопеременна.
Задание на понимание: у данной матрицы четыре главных минора 1-го порядка: 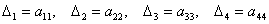
шесть главных миноров 2-го порядка: 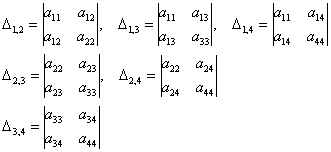
четыре главных минора 3-го порядка: 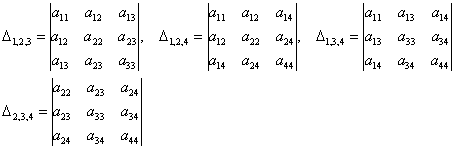
и один главный минор 4-го порядка, равный определителю матрицы.
Пример 5*. Решение: запишем матрицу формы 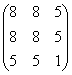
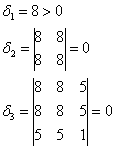
Таким образом, форма не удовлетворяет критерию Сильвестра, однако, может оказаться неотрицательной (т.к. 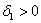
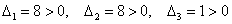
Вычислим главные миноры 2-го порядка:
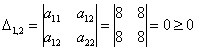
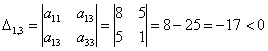
Ответ: форма знакопеременна.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5