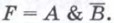что также называют логическим сложением
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.3. Элементы алгебры логики
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
1.3.1. Высказывание
Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.
Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.
В русском языке высказывания выражаются повествовательными предложениями. Но не всякое повествовательное предложение является высказыванием.
Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.
Побудительные и вопросительные предложения высказываниями не являются.
Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».
Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т. п.
Примерами высказываний могут служить:
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X
1.3.2. Логические операции
Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций.
Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.
Конъюнкция
Рассмотрим два высказывания: А = «Основоположником алгебры логики является Джордж Буль», В = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.
Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И, ∧, •, &.
Например: А И В, А ∧ В, А • В, А&В.
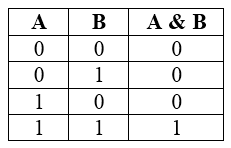
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:
В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Конъюнкцию также называют логическим умножением.
Дизъюнкция. Инверсия
Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использова ния в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ, ∨, |, +. Например: А ИЛИ В, A∨B, А|В, А+В.
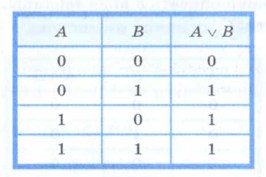
Дизъюнкция определяется следующей таблицей истинности:
Дизъюнкцию также называют логическим сложением. Подумайте почему.
Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
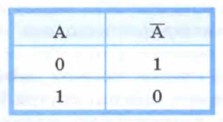
Инверсия определяется следующей таблицей истинности:
Инверсию также называют логическим отрицанием.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 8-х классов — отличники» является высказывание «Неверно, что все юноши 8-х классов — отличники», другими словами, «Не все юноши 8-х классов — отличники».
Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».
Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
Логические операции при выполнении имеют следующий приоритет: ин версия, конъюнкция, дизъюнкция.
1.3.2. Логические операции
Пример 1. Пусть А — «На web-странице встречается слово «крейсер»», В = «На web-странице встречается слово «линкор»». Рассматривается некоторый сегмент сети Интернет, содержащий 5 000 000 web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В — для 4500 страниц, а высказывание A ∨ В — для 7000 страниц. Для какого количества web-страниц в этом случае будут истинны следующие выражения и высказывание?
Решение. Изобразим множество всех web-страниц рассматриваемого сектора сети Интернет кругом, внутри которого разместим два круга: одному из них соответствует множество web-страниц, где истинно высказывание А, второму — где истинно высказывание В (рис. 1.3).
Изобразим графически множества web-страниц, для которых истинны выражения и высказывание а) — в) (рис. 1.4).
Построенные схемы помогут нам ответить на вопросы, содержащиеся в задании.
Выражение А ИЛИ В истинно для 7000 web-страниц, а всего страниц 5 000 000. Следовательно, выражение А ИЛИ В ложно для 4 993 000 web-страниц. Иначе говоря, для 4 993 000 web-страниц истинно выражение НЕ (А ИЛИ В).
Выражение A ∨ В истинно для тех web-страниц, где истинно А (4800), а также тех web-страниц, где истинно В (4500). Если бы все web-страницы были различны, то выражение A ∨ В было бы истинно для 9300 (4800 + 4500) web-страниц. Но, согласно условию, таких web-страниц всего 7000. Это значит, что на 2300 (9300 — 7000) web-страницах встречаются оба слова одновременно. Следовательно, выражение А & В истинно для 2300 web-страниц.
Чтобы выяснить, для скольких web-страниц истинно высказывание А и одновременно ложно высказывание В, следует из 4800 вычесть 2300. Таким образом, высказывание «На web-странице встречается слово «крейсер” И не встречается слово «линкор»» истинно на 2500 web-страницах.
Самостоятельно запишите логическое выражение, соответствующее рассмотренному выше высказыванию.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcoir.edu.ru/) размещён информационный модуль «Высказывание. Простые и сложные высказывания. Основные логические операции». Знакомство с этим ресурсом позволит вам расширить представления по изучаемой теме.
1.3.3. Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
Построим таблицу истинности для логического выражения A ∨ А & Б. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A ∨ А & В равносильно логической переменной А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства логических операций, называемых также законами алгебры логики.
1. Переместительный (коммутативный) закон:
2. Сочетательный (ассоциативный) закон:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
A ∨ (В & С) = (A ∨ В) & (A v С).
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
7. Законы операций с 0 и 1:
8. Законы общей инверсии:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Пример 2. Найдём значение логического выражения
Решение. При X = 0 получаем следующее логическое выражение:
Так как логические выражения 0
Элементы алгебры логики. Решение логических задач
Рассмотрим несколько способов решения логических задач.
Задача 1. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:
Бабушка знала, что один из её внуков, назовём его правдивым, оба раза сказал правду; второй, назовём его шутником, оба раза сказал неправду; третий, назовём его хитрецом, один раз сказал правду, а другой раз — неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?
Решение. Пусть К = «Коля разбил вазу», В = «Вася разбил вазу», С — «Серёжа разбил вазу». Для решения задачи можно составить таблицу истинности, в которой представить высказывания каждого мальчика. Так как ваза разбита одним внуком, то чтобы выяснить, кто именно это сделал, достаточно фрагмента таблицы истинности, содержащего наборы значений входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строку, содержащую в каком-либо порядке три комбинации значений: 00 (слова шутника), 11 (слова правдивого внука), 01 или 10 (слова хитреца). Такая строка отмечена галочкой. Согласно этой строке, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах? Решение. Рассмотрим простые высказывания:
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание C1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2 • С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, принять участие в интернет-олимпиадах и конкурсах по их решению вы сможете на российской странице международного математического конкурса «Кенгуру» (http://mathkang.ru/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента 0, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе F при каждом возможном наборе сигналов A и B на входах.
Решение. Все возможные комбинации сигналов А и Б на входах внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную 4 схему.
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа А и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov.narod.ru/prog/logic.htm).
Элементы алгебры логики. Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
§ 1.3. Элементы алгебры логики
§ 2.1. Алгоритмы и исполнители
1.3.2. Логические операции (продолжение)
Дизъюнкция. Инверсия
Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использова ния в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

 Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. |
Для записи дизъюнкции используются следующие знаки: ИЛИ, ∨, |, +. Например: А ИЛИ В, A∨B, А|В, А+В.
Дизъюнкция определяется следующей таблицей истинности:

Инверсия
 Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. |
Инверсия определяется следующей таблицей истинности:
Инверсию также называют логическим отрицанием.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 8-х классов — отличники» является высказывание «Неверно, что все юноши 8-х классов — отличники», другими словами, «Не все юноши 8-х классов — отличники».
Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
Логические операции и их свойства
Вы будете перенаправлены на Автор24
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Таблица истинности для конъюнкции
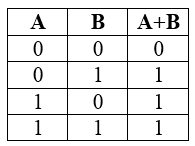
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Таблица истинности для дизъюнкции
Готовые работы на аналогичную тему
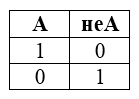
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Таблица истинности для инверсии
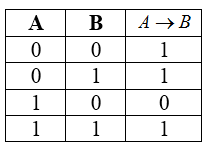
Импликация или логическое следование
Таблица истинности для импликации
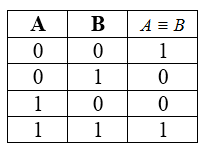
Эквивалентность или логическая равнозначность
Таблица истинности для эквивалентности
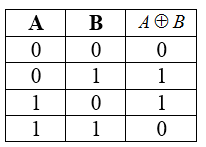
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Таблица истинности для операции сложения по модулю два
Свойства строгой дизъюнкции:
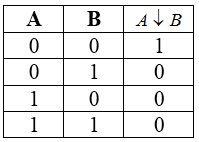
Стрелка Пирса
Таблица истинности для стрелки Пирса
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X \downarrow X = ¬X$— отрицание
$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция
$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция
$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
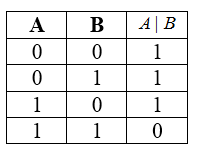
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Таблицей истинности для функции штрих Шеффера
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X \mid X = ¬X$ — отрицание
$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция
$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.